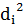|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Тема: «Описательная статистика. Показатели разнообразия признака в совокупности»Основными критериями разнообразия признака в статистической совокупности являются: лимит, амплитуда, среднее квадратическое отклонение, коэффициент осцилляции и коэффициент вариации. На предыдущем занятии обсуждалось, что средние величины дают лишь обобщающую характеристику изучаемого признака в совокупности и не учитывают значения отдельных его вариант: минимальное и максимальное значения, выше среднего, ниже среднего и т.д. Пример. Средние величины двух разных числовых последовательностей: -100; -20; 100; 20 и 0,1; -0,2; 0,1 абсолютно одинаковы и равны О. Однако, диапазоны разброса данных этих последовательностей относительного среднего значения сильно различны. Определение перечисленных критериев разнообразия признака прежде всего осуществляется с учетом его значения у отдельных элементов статистической совокупности. Показатели измерения вариации признака бывают абсолютные и относительные. К абсолютным показателям вариации относят: размах вариации, лимит, среднее квадратическое отклонение, дисперсию. Коэффициент вариации и коэффициент осцилляции относятся к относительным показателям вариации. Лимит (lim)– это критерий, который определяется крайними значениями вариант в вариационном ряду. Другими словами, данный критерий ограничивается минимальной и максимальной величинами признака:
Амплитуда (Am) или размах вариации – это разность крайних вариант. Расчет данного критерия осуществляется путем вычитания из максимального значения признака его минимального значения, что позволяет оценить степень разброса вариант:
Недостатком лимита и амплитуды как критериев вариабельности является то, что они полностью зависят от крайних значений признака в вариационном ряду. При этом не учитываются колебания значений признака внутри ряда.
Наиболее полную характеристику разнообразия признака в статистической совокупности дает среднее квадратическое отклонение В основе среднего квадратического отклонения лежит сопоставление каждой варианты
По смыслу, дисперсия – это средний квадрат отклонений индивидуальных значений признака от его средней величины. Дисперсия – квадрат среднего квадратического отклонения Дисперсия является размерной величиной (именованной). Так, если варианты числового ряда выражены в метрах, то дисперсия дает квадратные метры; если варианты выражены в килограммах, то дисперсия дает квадрат этой меры (кг2), и т.д. Среднее квадратическое отклонение – квадратный корень из дисперсии:
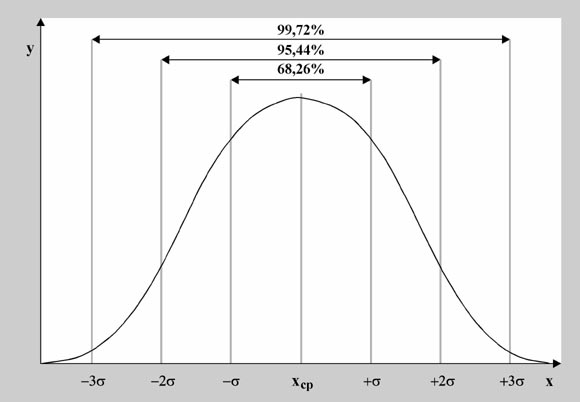
В том случае, если число элементов совокупности Расчет среднего квадратического отклонения можно разбить на шесть этапов, которые необходимо осуществить в определенной последовательности: 1. определить среднюю арифметическую M имеющейся совокупности 2. рассчитать отклонение каждой варианты от средней величины: 3. каждое отклонение возвести в квадрат: 4. посчитать сумму всех 5. разделить получившуюся сумму на число элементов совокупности n 6. из полученного результата извлечь квадратный корень Применение среднеквадратического отклонения: а) для суждения о колеблемости вариационных рядов и сравнительной оценки типичности (представительности) средних арифметических величин. Это необходимо в дифференциальной диагностике при определении устойчивости признаков. б) для реконструкции вариационного ряда, т.е. восстановления его частотной характеристики на основе правила «трех сигм». В интервале (М±3σ) находится 99,7% всех вариант ряда, в интервале (М±2σ) — 95,5% и в интервале (М±1σ) — 68,3% вариант ряда (рис.1). в) для выявления «выскакивающих» вариант г) для определения параметров нормы и патологии с помощью сигмальных оценок д) для расчета коэффициента вариации е) для расчета средней ошибки средней арифметической величины.
Для характеристики любой генеральной совокупности, имеющей нормальный тип распределения, достаточно знать два параметра: среднюю арифметическую и среднее квадратическое отклонение.
Рисунок 1. Правило «трех сигм» Дата добавления: 2014-12-11 | Просмотры: 1719 | Нарушение авторских прав |
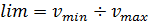
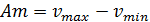
 (сигма), которое является общей мерой отклонения вариант от своей средней величины. Среднее квадратическое отклонение часто называют также стандартным отклонением.
(сигма), которое является общей мерой отклонения вариант от своей средней величины. Среднее квадратическое отклонение часто называют также стандартным отклонением. со средней арифметической
со средней арифметической  данной совокупности. Так как в совокупности всегда будут варианты как меньше, так и больше, чем она, то сумма отклонений
данной совокупности. Так как в совокупности всегда будут варианты как меньше, так и больше, чем она, то сумма отклонений  , имеющих знак "
, имеющих знак "  ", будет погашаться суммой отклонений, имеющих знак "
", будет погашаться суммой отклонений, имеющих знак "  ", т.е. сумма всех отклонений
", т.е. сумма всех отклонений  равна нулю. Для того, чтобы избежать влияния знаков разностей берут отклонения вариант от среднего арифметического в квадрате, т.е.
равна нулю. Для того, чтобы избежать влияния знаков разностей берут отклонения вариант от среднего арифметического в квадрате, т.е.  . Сумма квадратов отклонений не равняется нулю. Чтобы получить коэффициент, способный измерить изменчивость, берут среднее от суммы квадратов – это величина носит название дисперсии:
. Сумма квадратов отклонений не равняется нулю. Чтобы получить коэффициент, способный измерить изменчивость, берут среднее от суммы квадратов – это величина носит название дисперсии: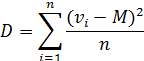
 .
.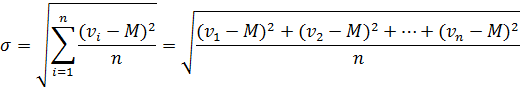
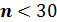 , то при расчете дисперсии и среднего квадратического отклонения в знаменателе дроби вместо
, то при расчете дисперсии и среднего квадратического отклонения в знаменателе дроби вместо  необходимо ставить
необходимо ставить  .
.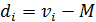
 (Для получения обобщающей характеристики числового ряда использовать сумму отклонений от среднего нельзя. Это связано с тем, что сумма всех отрицательных и положительных отклонений от среднего всегда равна нулю.)
(Для получения обобщающей характеристики числового ряда использовать сумму отклонений от среднего нельзя. Это связано с тем, что сумма всех отрицательных и положительных отклонений от среднего всегда равна нулю.)