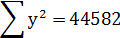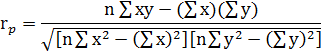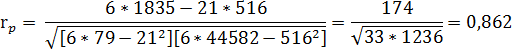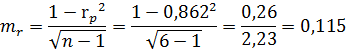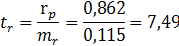|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Данные экзамена по статистике
Решение: Очевидно, что количество часов напрямую отражается на финальной оценке. Переменная «Часы подготовки» (х) является независимой переменной, т.к. она приводит к наблюдаемой вариации переменной «Балл на экзамене» (у). Причинная связь между зависимыми и независимыми переменными существует только в одном направлении: Независимая переменная (х)→ Зависимая переменная (у). В обратном направлении эта связь не работает. Коэффициент корреляции Пирсона (r) вычисляется при помощи следующего уравнения
Таблица, приведенная ниже, поможет разбить это уравнение на несколько несложных вычислений.
Используя эти значения и n=6 (общее количество студентов), получаем:
Теперь рассчитаем среднюю ошибку коэффициента корреляции
Установим, надежной, ли является установленная нами связь
Т.к. tr≥3, то коэффициент корреляции является статистически значимым. Таким образом, между числом часов, посвященных изучению предмета, и экзаменационной оценкой существует статистически значимая сильная положительная (прямая) корреляция. Отсюда следует, что экзаменационные результаты можно предугадать на основе определенного количества часов, посвященных изучению предмета.
Дата добавления: 2014-12-11 | Просмотры: 940 | Нарушение авторских прав |
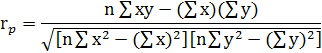
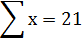
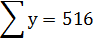
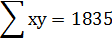
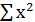 =79
=79