 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Оценка статистической значимости результатов исследованияПод статистической значимостью данных понимают степень их соответствия отображаемой действительности, т.е. статистически значимыми данными считаются те, которые не искажают и правильно отражают объективную реальность. Оценить статистическую значимость результатов исследования – означает определить, с какой вероятностью возможно перенести результаты, полученные на выборочной совокупности, на всю генеральную совокупность. Оценка статистической значимости необходима для понимания того, насколько по части явления можно судить о явлении в целом и его закономерностях. Оценка статистической значимости результатов исследования складывается из: 1. ошибок репрезентативности (ошибок средних и относительных величин) — m; 2. доверительных границ средних или относительных величин; 3. достоверности разности средних или относительных величин по критерию t. Стандартная ошибка средней арифметической или ошибка репрезентативности характеризует колебания средней. При этом необходимо отметить, что чем больше объем выборки, тем меньше разброс средних величин. Стандартная ошибка среднего вычисляется по формуле:
В современной научной литературе средняя арифметическая записывается вместе с ошибкой репрезентативности:
или вместе со среднеквадратическим отклонением:
В качестве примера рассмотрим данные по 1500 городских поликлиник страны (генеральная совокупность). Среднее число пациентов, обслуживающихся в поликлинике равно 18150 человек. Случайный отбор 10 % объектов (150 поликлиник) дает среднее число пациентов, равное 20051 человек. Ошибка выборки, очевидно связанная с тем, что не все 1500 поликлиник попали в выборку, равна разности между этими средними – генеральным средним (M ген) и выборочным средним (М выб). Если сформировать другую выборку того же объема из нашей генеральной совокупности, она даст другую величину ошибки. Все эти выборочные средние при достаточно больших выборках распределены нормально вокруг генеральной средней при достаточно большом числе повторений выборки одного и того же числа объектов из генеральной совокупности. Стандартная ошибка среднего m - это неизбежный разброс выборочных средних вокруг генеральной средней. В случае, когда результаты исследования представлены относительными величинами (например, процентными долями) – рассчитывается стандартная ошибка доли:
где P – показатель в %, n – количество наблюдений. Результат отображается в виде (P ± m)%. Например, процент выздоровления среди больных составил (95,2±2,5)%. В том случае, если число элементов совокупности
Для нормального распределения (распределение выборочных средних является нормальным) известно, какая часть совокупности попадает в любой интервал вокруг среднего значения. В частности: · 68,3% всех выборочных средних попадают в интервал · 95,5% - в интервал · 99,7% - в интервал На практике проблема заключается в том, что характеристики генеральной совокупности нам неизвестны, а выборка делается именно с целью их оценки. Это означает, что если мы будем делать выборки одного и того же объема n из генеральной совокупности, то в 68,3% случаев на интервале будет находиться значение M (оно же в 95,5% случаев будет находиться на интервале и в 99,7% случаев – на интервале). Поскольку реально делается только одна выборка, то формулируется это утверждение в терминах вероятности: с вероятностью 68,3% среднее значение признака в генеральной совокупности заключено в интервале, с вероятностью 95,5% - в интервале и т.д. На практике вокруг выборочного значения строится такой интервал, который бы с заданной (достаточно высокой) вероятностью – доверительной вероятностью – «накрывал» бы истинное значение этого параметра в генеральной совокупности. Этот интервал называется доверительным интервалом. Доверительная вероятность P – это степень уверенности в том, что доверительный интервал действительно будет содержать истинное (неизвестное) значение параметра в генеральной совокупности. Например, если доверительная вероятность Р равна 90%, то это означает, что 90 выборок из 100 дадут правильную оценку параметра в генеральной совокупности. Соответственно, вероятность ошибки, т.е. неверной оценки генерального среднего по выборке, равна в процентах: Очевидно, что степень уверенности (доверительная вероятность) зависит от величины интервала: чем шире интервал, тем выше уверенность, что в него попадет неизвестное значение для генеральной совокупности. На практике для построения доверительного интервала берется, как минимум, удвоенная ошибка выборки, чтобы обеспечить уверенность не менее 95,5%. Определение доверительных границ средних и относительных величин позволяет найти два их крайних значения – минимально возможное и максимально возможное, в пределах которых изучаемый показатель может встречаться во всей генеральной совокупности. Исходя из этого, доверительные границы (или доверительный интервал) - это границы средних или относительных величин, выход за пределы которых вследствие случайных колебаний имеет незначительную вероятность. Доверительный интервал может быть переписан в виде: Доверительные границы средней арифметической величины в генеральной совокупности определяют по формуле: Мген = Мвыб + t mM для относительной величины: Рген = Рвыб + t mР где Мген и Рген - значения средней и относительной величины для генеральной совокупности; Мвыб и Рвыб - значения средней и относительной величины, полученные на выборочной совокупности; mM и mP - ошибки средней и относительной величин; t - доверительный критерий (критерий точности, который устанавливается при планировании исследования и может быть равен 2 или 3); t m - это доверительный интервал или Δ – предельная ошибка показателя, полученного при выборочном исследовании. Следует отметить, что величина критерия t в определенной мере связана с вероятностью безошибочного прогноза (р), выраженной в %. Ее избирает сам исследователь, руководствуясь необходимостью получить результат с нужной степенью точности. Так, для вероятности безошибочного прогноза 95,5% величина критерия t составляет 2, для 99,7% - 3. Приведенные оценки доверительного интервала приемлемы лишь для статистических совокупностей с количеством наблюдений более 30. При меньшем объеме совокупности (малых выборках) для определения критерия t пользуются специальными таблицами. В данных таблицах искомое значение находится на пересечении строки, соответствующей численности совокупности (n-1), и столбца, соответствующего уровню вероятности безошибочного прогноза (95,5%; 99,7%), выбранному исследователем. В медицинских исследованиях при установлении доверительных границ любого показателя принята вероятность безошибочного прогноза 95,5% и более. Это означает, что величина показателя, полученная на выборочной совокупности должна встречаться в генеральной совокупности как минимум в 95,5% случаев. 1. Вопросы по теме занятия: 1. Актуальность показателей разнообразия признака в статистической совокупности. 2. Общая характеристика абсолютных показателей вариации. 3. Среднее квадратическое отклонение, расчет, применение. 4. Относительные показатели вариации. 5. Медиана, квартильная оценка. 6. Оценка статистической значимости результатов исследования. 7. Стандартная ошибка средней арифметической, формула расчета, пример использования. 8. Расчет доли и ее стандартной ошибки. 9. Понятие доверительной вероятности, пример использования. 10. Понятие доверительного интервала, его применение.
2. Тестовые задания по теме с эталонами ответов:
1. К АБСОЛЮТНЫМ ПОКАЗАТЕЛЯМ ВАРИАЦИИ ОТНОСИТСЯ 1) коэффициент вариации 2) коэффициент осцилляции 3) лимит 4) медиана
2. К ОТНОСИТЕЛЬНЫМ ПОКАЗАТЕЛЯМ ВАРИАЦИИ ОТНОСИТСЯ 1) дисперсия 2) лимит 3) среднее квадратичное отклонение 4) коэффициент вариации 3. КРИТЕРИЙ, КОТОРЫЙ ОПРЕДЕЛЯЕТСЯ КРАЙНИМИ ЗНАЧЕНИЯМИ ВАРИАНТ В ВАРИАЦИОННОМ РЯДУ 1) лимит 2) амплитуда 3) дисперсия 4) коэффициент вариации
4. РАЗНОСТЬ КРАЙНИХ ВАРИАНТ – ЭТО 1) лимит 2) амплитуда 3) среднее квадратичное отклонение 4) коэффициент вариации
5. СРЕДНИЙ КВАДРАТ ОТКЛОНЕНИЙ ИНДИВИДУАЛЬНЫХ ЗНАЧЕНИЙ ПРИЗНАКА ОТ ЕГО СРЕДНЕЙ ВЕЛИЧИНЫ – ЭТО 1) коэффициент осцилляции 2) медиана 3) дисперсия 4) мода
6. ОТНОШЕНИЕ РАЗМАХА ВАРИАЦИИ К СРЕДНЕЙ ВЕЛИЧИНЕ ПРИЗНАКА – ЭТО 1) коэффициент вариации 2) среднее квадратичное отклонение 3) лимит 4) коэффициент осцилляции
7. ОТНОШЕНИЕ СРЕДНЕГО КВАДРАТИЧНОГО ОТКЛОНЕНИЯ К СРЕДНЕЙ ВЕЛИЧИНЕ ПРИЗНАКА – ЭТО 1) дисперсия 2) коэффициент вариации 3) коэффициент осцилляции 4) амплитуда
8. ВАРИАНТА, КОТОРАЯ НАХОДИТСЯ В СЕРЕДИНЕ ВАРИАЦИОННОГО РЯДА И ДЕЛИТ ЕГО НА ДВЕ РАВНЫЕ ЧАСТИ – ЭТО 1) медиана 2) мода 3) амплитуда 4) лимит
9. В МЕДИЦИНСКИХ ИССЛЕДОВАНИЯХ ПРИ УСТАНОВЛЕНИИ ДОВЕРИТЕЛЬНЫХ ГРАНИЦ ЛЮБОГО ПОКАЗАТЕЛЯ ПРИНЯТА ВЕРОЯТНОСТЬ БЕЗОШИБОЧНОГО ПРОГНОЗА 1) 80% 2) 68% 3) 95% 4) 50%
10. ЕСЛИ 90 ВЫБОРОК ИЗ 100 ДАЮТ ПРАВИЛЬНУЮ ОЦЕНКУ ПАРАМЕТРА В ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ, ТО ЭТО ОЗНАЧАЕТ, ЧТО ДОВЕРИТЕЛЬНАЯ ВЕРОЯТНОСТЬ P РАВНА 1) 10% 2) 90% 3) 68% 4) 50%
11. В СЛУЧАЕ, ЕСЛИ 10 ВЫБОРОК ИЗ 100 ДАЮТ НЕВЕРНУЮ ОЦЕНКУ, ВЕРОЯТНОСТЬ ОШИБКИ РАВНА 1) 90% 2) 50% 3) 20% 4) 10%
12. ГРАНИЦЫ СРЕДНИХ ИЛИ ОТНОСИТЕЛЬНЫХ ВЕЛИЧИН, ВЫХОД ЗА ПРЕДЕЛЫ КОТОРЫХ ВСЛЕДСТВИЕ СЛУЧАЙНЫХ КОЛЕБАНИЙ ИМЕЕТ НЕЗНАЧИТЕЛЬНУЮ ВЕРОЯТНОСТЬ – ЭТО 1) доверительный интервал 2) амплитуда 3) лимит 4) коэффициент вариации
13. МАЛОЙ ВЫБОРКОЙ СЧИТАЕТСЯ ТА СОВОКУПНОСТЬ, В КОТОРОЙ 1) n меньше или равно 100 2) n меньше или равно 30 3) n меньше или равно 40 4) n близко к 0
14. ДЛЯ ВЕРОЯТНОСТИ БЕЗОШИБОЧНОГО ПРОГНОЗА 95% ВЕЛИЧИНА КРИТЕРИЯ t СОСТАВЛЯЕТ 1) 3 2) 2 3) 1 4) 10
15. ДЛЯ ВЕРОЯТНОСТИ БЕЗОШИБОЧНОГО ПРОГНОЗА 99% ВЕЛИЧИНА КРИТЕРИЯ t СОСТАВЛЯЕТ 1) 3 2) 2 3) 1 4) 5
16. ДЛЯ РАСПРЕДЕЛЕНИЙ, БЛИЗКИХ К НОРМАЛЬНОМУ, СОВОКУПНОСТЬ СЧИТАЕТСЯ ОДНОРОДНОЙ, ЕСЛИ КОЭФФИЦИЕНТ ВАРИАЦИИ НЕ ПРЕВЫШАЕТ 1) 50% 2) 10% 3) 33% 4) 90%
17. ВАРИАНТА, ОТДЕЛЯЮЩАЯ ВАРИАНТЫ, ЧИСЛОВЫЕ ЗНАЧЕНИЯ КОТОРЫХ НЕ ПРЕВЫШАЮТ 25% МАКСИМАЛЬНО ВОЗМОЖНОГО В ДАННОМ РЯДУ – ЭТО 1) мода 2) нижний квартиль 3) верхний квартиль 4) квартиль
18. ДАННЫЕ, КОТОРЫЕ НЕ ИСКАЖАЮТ И ПРАВИЛЬНО ОТРАЖАЮТ ОБЪЕКТИВНУЮ РЕАЛЬНОСТЬ, НАЗЫВАЮТСЯ 1) невозможные 2) равновозможные 3) достоверные 4) случайные
19. СОГЛАСНО ПРАВИЛУ "ТРЕХ СИГМ", ПРИ НОРМАЛЬНОМ РАСПРЕДЕЛЕНИИ ПРИЗНАКА В ПРЕДЕЛАХ 1) 68,3% вариант 2) 95,5% вариант 3) 99,7% вариант 4) 50,0% вариант
20. ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ, СООТВЕТСТВУЮЩИЙ СТЕПЕНИ ВЕРОЯТНОСТИ 1) 67% 2) 68,3% 3) 95,5% 4) 99,7%
21. КОЭФФИЦИЕНТ ВАРИАЦИИ ПРИМЕНЯЕТСЯ 1) для характеристики нормальности распределения 2) для характеристики однородности совокупности 3) для определения среднеквадратического отклонения 4) для определения необходимого объема выборки
22. ВАРИАНТА, ОТДЕЛЯЮЩАЯ ВАРИАНТЫ ВЕЛИЧИНОЙ ДО 75% ОТ МАКСИМАЛЬНО ВОЗМОЖНЫХ ЗНАЧЕНИЙ – ЭТО 1) нижний квартиль 2) мода 3) верхний квартиль 4) квартиль
23. ВАРИАНТА, ОТДЕЛЯЮЩАЯ ВАРИАНТЫ С ЧИСЛОВЫМ ЗНАЧЕНИЕМ ДО 50% ОТ МАКСИМАЛЬНО ВОЗМОЖНОГО – ЭТО 1) квартиль 2) нижний квартиль 3) мода 4) верхний квартиль
24 КОЭФФИЦИЕНТ ВАРИАЦИИ ВЫРАЖАЕТСЯ 1) в сантиметрах 2) в числе пациентов 3) в числе вариаций 4) в процентах
25. В СЛУЧАЕ СИММЕТРИЧНОСТИ РАСПРЕДЕЛЕНИЯ ОТНОСИТЕЛЬНО СРЕДНЕГО АРИФМЕТИЧЕСКОГО ДЛЯ ЕГО ХАРАКТЕРИСТИКИ ИСПОЛЬЗУЮТСЯ 1) медиана и процентили 2) лимит и среднеквадратичное отклонение 3) среднее арифметическое и среднеквадратичное отклонение 4) среднее арифметическое и процентили
26. В СЛУЧАЕ АСИММЕТРИЧНОСТИ РАСПРЕДЕЛЕНИЯ ОТНОСИТЕЛЬНО СРЕДНЕГО АРИФМЕТИЧЕСКОГО ДЛЯ ЕГО ХАРАКТЕРИСТИКИ ИСПОЛЬЗУЮТСЯ 1) медиана и процентили 2) медиана и среднеквадратичное отклонение 3) среднее арифметическое и среднеквадратичное отклонение 4) среднее арифметическое и процентили
27. ПРИ ЗНАЧЕНИИ КОЭФФИЦИЕНТА ВАРИАЦИИ 15% СТЕПЕНЬ РАЗНООБРАЗИЯ ПРИЗНАКА ОЦЕНИВАЕТСЯ КАК 1) слабая 2) средняя 3) сильная 4) равномерная
28. ГРАНИЦЫ СРЕДНИХ ИЛИ ОТНОСИТЕЛЬНЫХ ВЕЛИЧИН, ВЫХОД ЗА ПРЕДЕЛЫ КОТОРЫХ ВСЛЕДСТВИЕ СЛУЧАЙНЫХ КОЛЕБАНИЙ ИМЕЕТ НЕЗНАЧИТЕЛЬНУЮ ВЕРОЯТНОСТЬ – ЭТО 1) доверительный интервал 2) доверительный критерий 3) стандартная ошибка 4) среднее квадратическое отклонение
29. ДЛЯ РАСЧЕТА КОЭФФИЦИЕНТА ВАРИАЦИИ НЕОБХОДИМА СЛЕДУЮЩАЯ ВЕЛИЧИНА 1) стандартная ошибка 2) медиана 3) среднее квадратическое отклонение 4) доверительный интервал
30. НЕДОСТАТКОМ ЛИМИТА И АМПЛИТУДЫ КАК КРИТЕРИЕВ ВАРИАБЕЛЬНОСТИ ЯВЛЯЕТСЯ 1) необходимость нормального распределения для их расчета 2) зависимость от крайних значений переменных 3) зависимость от числа наблюдений 4) зависимость от средних значений переменных
Эталоны ответов на тестовые задания:
Дата добавления: 2014-12-11 | Просмотры: 2055 | Нарушение авторских прав |
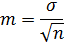
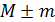
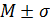
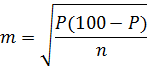
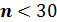 , то при расчете стандартных ошибок среднего и доли в знаменателе дроби вместо
, то при расчете стандартных ошибок среднего и доли в знаменателе дроби вместо  необходимо ставить
необходимо ставить  .
.
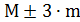
 . Для данного примера это значит, что 10 выборок из 100 дадут неверную оценку.
. Для данного примера это значит, что 10 выборок из 100 дадут неверную оценку. , где t – доверительный критерий.
, где t – доверительный критерий.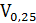
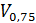
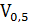
 БУДЕТ НАХОДИТЬСЯ
БУДЕТ НАХОДИТЬСЯ (n>30), СОСТАВЛЯЕТ
(n>30), СОСТАВЛЯЕТ