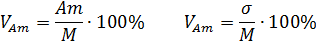|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Пример. В педиатрии среднеквадратическое отклонение используется для оценки физического развития детей путем сравнения данных конкретного ребенка с соответствующими
В педиатрии среднеквадратическое отклонение используется для оценки физического развития детей путем сравнения данных конкретного ребенка с соответствующими стандартными показателями. За стандарт принимаются средние арифметические показатели физического развития здоровых детей. Сравнение показателей со стандартами проводят по специальным таблицам, в которых стандарты приводятся вместе с соответствующими им сигмальными шкалами. Считается, что если показатель физического развития ребенка находится в пределах стандарт (среднее арифметическое) ±σ, то физическое развитие ребенка (по этому показателю) соответствует норме. Если показатель находится в пределах стандарт ±2σ, то имеется незначительное отклонение от нормы. Если показатель выходит за эти границы, то физическое развитие ребенка резко отличается от нормы (возможна патология). Кроме показателей вариации, выраженных в абсолютных величинах, в статистическом исследовании используются показатели вариации, выраженные в относительных величинах. Коэффициент осцилляции -это отношение размаха вариации к средней величине признака. Коэффициент вариации - это отношение среднего квадратического отклонения к средней величине признака. Как правило, эти величины выражаются в процентах. Формулы расчета относительных показателей вариации:
Из приведенных формул видно, что чем больше коэффициент V приближен к нулю, тем меньше вариация значений признака. Чем больше V, тем более изменчив признак. В статистической практике наиболее часто применяется коэффициент вариации. Он используется не только для сравнительной оценки вариации, но и для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному). Арифметически отношение σ и средней арифметической нивелирует влияние абсолютной величины этих характеристик, а процентное соотношение делает коэффициент вариации величиной безразмерной (неименованной). Полученное значение коэффициента вариации оценивается в соответствии с ориентировочными градациями степени разнообразия признака: - слабое — до 10 % - среднее — 10 - 20 % - сильное — более 20 % Использование коэффициента вариации целесообразно в случаях, когда приходится сравнивать признаки разные по своей величине и размерности. Отличие коэффициента вариации от других критериев разброса наглядно демонстрирует пример. Таблица 1 Состав работников промышленного предприятия
На основании приведенных в примере статистических характеристик можно сделать вывод об относительной однородности возрастного состава и образовательного уровня работников предприятия при низкой профессиональной устойчивости обследованного контингента. Нетрудно заметить, что попытка судить об этих социальных тенденциях по среднему квадратическому отклонению привела бы к ошибочному заключению, а попытка сравнения учетных признаков «стаж работы» и «возраст» с учетным признаком «образование» вообще была бы некорректной из-за разнородности этих признаков. Дата добавления: 2014-12-11 | Просмотры: 949 | Нарушение авторских прав |