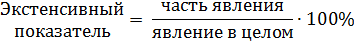|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Относительные величины. Статистические коэффициенты
В медицине и здравоохранении могут использоваться как абсолютные, так и относительные величины. Абсолютные величины характеризуют показатели на определенный момент времени (моментные) или за период (интервальные). На момент времени абсолютные величины показывают состояние явления (численность населения, уровень артериального давления, показание температуры тела); за период – явление за определенный промежуток времени (количество заболевших за неделю, число вызовов скорой помощи за месяц). Абсолютные величины всегда представляются в именованных единицах измерения (сантиметры, килограммы, дни и т. п.). Относительные величины представляют собой отношение двух абсолютных показателей и, соответственно, не имеют размерности. Они вычисляются в том случае, когда необходимо сравнить явления, происходящие одновременно или отстоящие друг от друга по времени (пример: сравнение заболеваемости населения в г.Красноярске и заболеваемости в г.Ачинске; сравнение уровней рождаемости 2000 и 2011 гг.). Относительные величины широко используются в официальной статистике для оценки медико-демографической и санитарно-эпидемиологической ситуации, оценки деятельности медицинских учреждений и т.п. Среди относительных величин наибольшее практическое значение имеют: интенсивные коэффициенты, экстенсивные коэффициенты, показатели соотношения, показатели наглядности, показатели относительной интенсивности. Интенсивные коэффициенты показывают интенсивность развития (частоту, уровень, распространенность, риск) явления в среде, которая продуцирует это явление. Эти коэффициенты отвечают на вопрос, как часто явление встречается в известной среде. Например: явление – количество заболевших за год относим к среде, его продуцирующей – численности населения. Общая формула для расчета интенсивного показателя выглядит следующим образом:
Масштабирующий коэффициент применяется для удобства интерпретации полученных результатов. Его размер тем больше, чем меньше расчетное значение относительной величины. Масштабирующий коэффициент может принимать различные значения: 100, 1000, 10000 и т.д., и отражает численность населения, на которую рассчитывается показатель. Чем реже явление встречается в среде, тем большее значение масштабирующего коэффициента приходится выбирать. В ряде случаев принято использовать определенные масштабирующие показатели; например: общая заболеваемость всегда рассчитывается на 1000 человек населения. Выбор множителя для показателя обусловлен удобством пользования результатами вычислений. Например, при соотношении количества умерших от инфаркта миокарда за год к общей численности населения получим 0,000013. Если в этом примере считать на 1000 населения, то получим 0,13 случаев смерти от инфаркта миокарда на 1000 населения, если на 100 — 0,0013 случая на 100 человек. В данном примере разумнее всего в качестве множителя использовать 100 000, т. к. при этом получается удобное для восприятия число 13. Иногда для обозначения множителя используют сокращенные обозначения. Если показатель вычислялся на 100 — проценты (%), если на 1000 — промилле ( Вычисление и анализ этих коэффициентов является основой медицинских исследований, проводимых на уровне больших групп населения, населенных пунктов, городских и сельских районов, областей и регионов.
Пример В таб. 1 представлены данные о числе смертей в городе N. На основании этих данных можно сделать вывод о снижении смертности населения города N на 800 случаев (с 10000 до 9200). Однако, за указанный период времени, с 1980 по 2005 год, численность жителей города уменьшилась, соответственно, с 1 000 000 до 850 000 человек. Таблица 1
Если теперь пересчитать смертность в относительных показателях, то окажется, что смертность населения не уменьшилась, а возросла с 10,0 до 10,8 случаев на 1000 (масштабирующий коэффициент) жителей города.
Одной из самых грубых ошибок, допускаемых при вычислении статистических коэффициентов, является несоблюдение единства времени для исходных данных (например, нельзя рассчитывать относительные величины, используя количество заболевших или умерших за один год, а численность населения – за другой).
Аналогичным образом вычисляются специальные интенсивные показатели ( когда речь идет об определенной причине заболеваемости или смертности ). Например, если число умерших от туберкулеза в городе N составило в 2005 году 9, то показатель смертности от туберкулеза составит (9 / 850000 х 100 000), 1,1 случая на 100 000 жителей. Одной из особенностей интенсивных коэффициентов является невозможность их прямого сложения между собой (поскольку это дроби с разными знаменателями). Интенсивные величины используются для: а) определения уровня частоты, либо распространенности того или иного явления; б) сравнения ряда различных совокупностей по степени частоты того или иного явления; в) динамического анализа изучаемого явления. Для графического представления интенсивных коэффициентов используются различные варианты столбиковых и линейных диаграмм. Для отображения циклических явлений наглядными являются радиальные диаграммы. Экстенсивные коэффициенты характеризуют долю части явления по отношению к явлению в целом и отражают его структуру. Они всегда выражаются в процентах. Пример: из общего количества госпитализированных в хирургическое отделение 35% пришлось на больных с острым аппендицитом, 25% - на больных с паховой грыжей, 20% - на больных с желчекаменной болезнью, 15% - на больных с осложнениями язвенной болезни желудка, 5% - на больных с другими диагнозами. Экстенсивные коэффициенты характеризуют отношение части статистической совокупности к целой совокупности (долю, удельный вес, часть от целого), т.е. отношение отдельного элемента к итогу:
Пример Рассмотрим структуру причин смерти в Красноярском крае в 2009 году. Для графического представления экстенсивных коэффициентов используют внутрисекторную или внутристолбиковую диаграммы.
Рис. 1. Структура причин смертности в Красноярском крае в 2009г. Внутрисекторная диаграмма. При расчете экстенсивного показателя, как показателя структуры, сумма всех значений должна быть равна 100%. Экстенсивные величины используются для: а) определения удельного веса, части явления по отношению к явлению в целом; б) для определения структуры явления (например, возрастно-половая структура населения). Одной из самых распространенных ошибок, встречающихся в практике статистического анализа, является ошибочное использование интенсивных и экстенсивных коэффициентов. Экстенсивные величины не должны использоваться при сравнении явления во времени, а также при сравнении показателей в заведомо разных совокупностях. Коэффициенты соотношения применяются, когда приходится оценивать взаимосвязь разнородных величин. В медицинской практике показатели соотношения используются для оценки обеспеченности населения различными видами медицинской помощи. Например: обеспеченность населения больничными койками, соотношение средних медицинских работников и врачей, обеспеченность населения врачами и т.д. Коэффициенты соотношения, как и интенсивные коэффициенты, вычисляются через пропорцию. Могут вычисляться на 100, на 1000, на 10 000. В отличие от интенсивных коэффициентов они могут выражаться дробными числами, в которых дробная часть содержит одинаковое или большее количество значащих цифр, чем целая: 1,53 медсестры на 1 врача. Дата добавления: 2014-12-11 | Просмотры: 2209 | Нарушение авторских прав |

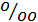 ), на 10 000 — продецимилле (
), на 10 000 — продецимилле (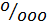 ) и т.д. При этом интенсивный показатель всегда остается величиной именованной (случаи заболеваний, рождений, смертей и т.п.).
) и т.д. При этом интенсивный показатель всегда остается величиной именованной (случаи заболеваний, рождений, смертей и т.п.).