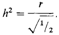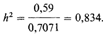|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Один пример: рост
Примером биометрического анализа, в котором осуществлена оценка наследуемости, является классическая работа Гальтона по наследованию роста (данные из работы Йохансена [726]). Он измерил рост 204 супружеских пар и 928 их взрослых детей. Имелось, однако, одно методологическое осложнение, состоящее в том, что рост женщин в среднем меньше, чем рост мужчин. Гальтон преодолел эту трудность, умножив все измерения женщин на 1,08, приведя их, таким образом, в соответствие с измерениями мужчин: 3. Формальная генетика человека 245
средний рост мужчин в его выборке был в 1,08 раз больше, чем средний рост женщин. Проведя такую коррекцию, он определил для каждой супружеской пары значение среднего родителя: ½ (♂ + ♀). Результат исследования виден в корреляции данных из табл. 3.17. Корреляция очевидна уже на первый взгляд, и ее величина оказалась достаточно высокой: r рс = 0,59 p < 0,01,где r рсобозначает корреляцию «средний родитель—ребенок». Это значение можно использовать для вычисления h2. Наследуемость равна
При случайном скрещивании это дает
Очевидно, что рост в основном детерминирован генетически, но существует компонента величиной 0,166 = 1 — 0,834, не учитываемая аддитивной генетической дисперсией. Это может быть следствием главным образом «средовых факторов». Говорят ли эти данные о каком-либо влиянии среды? Те же данные можно представить иначе (табл. 3.17 и 3.18). Иным в этом случае будет и характер расхождения с теоретически ожидаемыми значениями. При аддитивном действии генов среднее значение признака у детей должно быть равно полусумме родительских значений, т.е. должно совпадать со средним значением признака у родителей. Однако это не так, имеющиеся данные обнаруживают другую закономерность: если среднее значение признака у родителей выше популяционной средней, то среднее значение признака у детей оказывается меньше родительской средней. С другой стороны, если среднеродительское значение ниже популяционной средней, то среднее значение признака у детей выше такового среди родителей. Итак, среднее значение признака у детей имеет тенденцию к отклонению от родительской средней в направлении популяционной средней. Это явление было описано Гальтоном и названо им «регрессией на среднюю». Оно имеет место и для других непрерывно распределенных признаков (рис. 3.56). Какова же причина такого расхождения с теоретически ожидаемыми значениями? Вероятно, те индивиды, которые «располагаются» на периферии кривой распределения, несут генетические факторы, обусловливающие крайний фенотип, и, кроме того, находятся под влиянием необычных условий среды. Можно предположить также, что за проявление крайних фенотипов ответственны специфические межгенные взаимодействия и взаимодействия генов и среды. Маловероятно, что дети таких индивидов извлекут пользу из тех условий среды и генотип-средового взаимодействия, которые «поместили» их родителей в крайние классы распределения. Гораздо более вероятно, что фенотипические значения признака у детей будут в большей степени походить на популяционную среднюю, т. е. будет иметь место регрессия на среднюю. Дата добавления: 2015-12-16 | Просмотры: 715 | Нарушение авторских прав |