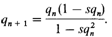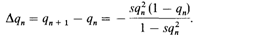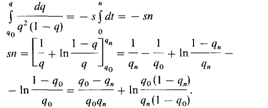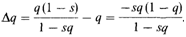|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Отбор, приводящий к изменению генных частот в одном направленииИспользуемые символы. Приспособленность генотипа определяется как его способность производить потомство. Она измеряется не в абсолютных, а в относительных единицах, причем приспособленность оптимального генотипа принимается равной единице. Отклонения от единицы обозначаются через s. Например, если приспособленность генотипа составляет 80% от приспособленности оптимального генотипа (s = 0,2), приспособленность этого генотипа равна 1 -s = 1 — 0,2 = 0,8. Чтобы избежать путаницы со знаками, иногда удобно использовать непосредственную меру приспособленности 1 — s = w. Иногда в литературе s определяется не относительно оптимальной, а относительно средней приспособленности популяции w. Такое обозначение не очень удачно, так как в этом случае приспособленность генотипа изменяется в зависимости от распределения генотипов в популяции. Поэтому мы будем определять приспособленность по отношению к «оптимальному» генотипу. Элиминация гетерозиготного «доминантного» фенотипа. Этот случай простой и встречается часто: какая-либо мутация изменяет фенотип ее носителя так сильно, что его размножение полностью прекращается. К таким последствиям у человека приво- 6. Популяционная генетика 297 дят все нарушения числа хромосом, большинство хромосомных аберраций и многие доминантные генные мутации (разд. 5.1.3). Хромосомные аберрации обнаруживаются прямым методом, однако вновь возникающие доминантные мутации можно выявить только в том случае, если они передаются потомству. Следовательно, доминантные мутации, приводящие к потере репродуктивной способности, невозможно обнаружить. О ее присутствии можно судить только на основании обследования тех немногочисленных индивидов, которые все же дали потомство, или по эффекту отцовского возраста. Возможно, что некоторые болезни и врожденные аномалии вызываются такими до сих пор не выявленными доминантными мутациями. Частичная элиминация аутосомных доминантных мутаций. Большинство вызываемых доминантными мутациями заболеваний уменьшает среднюю репродуктивную способность их носителей. В отсутствие противодействующих факторов, таких как мутационный процесс, эта потеря генов приводит в каждом поколении к уменьшению генных частот на некоторую величину, которая зависит от интенсивности отбора против носителей мутации (рис. 6.8). Пусть р- частота доминантного аллеля A, a q — частота рецессивного нормального аллеля а. Пусть отбор идет с достаточно высокой интенсивностью, а скорость мутирования μ
низка (разд. 5.3.1). Тогда гомозиготами АА можно пренебречь, поскольку их частота р2 очень низка. Частоты генотипов равны:
Элиминация особей Аа из популяции на поколение равна приблизительно 2ps. Поскольку только половина их генов - А, утрата генов А на поколение составляет 1/2(2 ps)= ps. Генетическое равновесие поддерживается, если эта утрата компенсируется возникновением мутаций: ps = μ (l -p)≈ μ. Отсюда равновесная частота р
Интересны два крайних случая: 1) Гетерозиготы не размножаются, т. е. s=1, w21 = 0. В соответствии с выводом, сделанным нами в предыдущем разделе, частота доминантного аллеля р будет равна скорости мутирования μ. 2) Ген не является селективно невыгодным (т.е. s = 0, w21 = 1). При таких условиях равновесие не возникает; частота доминантного аллеля монотонно возрастает: μ/s ®∞ 3) наконец, рассмотрим промежуточный случай, когда доминантный ген испытывает некоторое давление направленного против него отбора, например s = 1/3, w21 = 2/3; конечная частота доминантного гена будет равна утроенной скорости мутирования. Против большинства патологий действует отбор определенной интенсивности. Их частота в популяции определяется равновесием между мутационным процессом и отбором. Конечно, определяющим фактором здесь является скорость мутирования. Частота заболевания растет до тех пор, пока число пораженных индивидов не уве- 298 6. Популяционная генетика дичится настолько, что интенсивность направленного против них отбора уравновесит скорость мутирования и будет достигнуто генетическое равновесие. Это равновесие стабильно. Если число пораженных превысит равновесную величину, утрата неблагоприятного аллеля в результате отбора будет происходить быстрее его возникновения путем мутирования, и в следующем поколении его частота уменьшится. С другой стороны, если число больных станет ниже равновесной величины, мутационный процесс приведет к появлению большего числа неблагоприятных генов, чем то количество, которое отметается естественным отбором, и частота гена будет увеличиваться, пока вновь не установится равновесие. Ослабление отбора. Уравнение 6.1 можно использовать для определения последствий релаксации отбора. Предположим, что в результате медицинского вмешательства некоторые фенотипические проявления доминантной мутации были устранены, что привело к снижению селективной невыгодности аллеля с s 1= 1/2 до s2 = ¼. Пусть
Следовательно, новая частота равна удвоенной старой. Новое равновесие будет достигнуто через несколько поколений. Ослабление отбора против ретинобластомы. Ретинобластома — это злокачественная опухоль глаза, поражающая детей раннего возраста. Подавляющее большинство случаев возникновения ретинобластомы в популяциях являются спорадическими. Однако заболевание часто встречается в семьях и имеет аутосомное доминантное наследование с 90%-ной пенетрантностью. Все билатеральные, но только 10-12% унилатеральных спорадических случаев обусловлены вновь возникающими мутациями. В прежнее время ретинобластома почти всегда приводила к фатальному исходу: больные погибали в детском возрасте. В 1865 г. ван Графе впервые применил энуклеацию пораженного глаза; позднее в практику были введены дополнительные терапевтические меры - рентгеновское облучение и коагуляция светом; в настоящее время около 90% больных с унилатеральным и 80% больных с билатеральным поражениями могут вылечиться и иметь детей [1887]. Из всех вновь возникающих мутаций, определяющих наследственную форму ретинобластомы, 68% вызывают билатеральный и 32% унилатеральный тип поражения. Изменение частоты этого заболевания можно прогнозировать следующим образом. Путь Хо-частота больных наследственной регинобластомой в популяции; поскольку это заболевание очень редкое, частотой гомозигот можно пренебречь, а частоту нормального аллеля принять за q к 1; тогда Хо почти равна частоте гетерозигот (2pq s 2p). Пусть перед релаксацией отбора st = 1. После появления эффективных методов лечения давление отбора в случае унилатеральной формы стало sv = 0,1 (только 10% больных унилатеральной формой ретинобластомы умирают в детском возрасте; 90% из них выживают и имеют потомство); давление отбора в случае билатеральной формы sB = 0,2 (80% больных выживают и имеют потомство). Отсюда получаем следующую суммарную оценку s2 (сохранившийся после релаксации отбор против ретинобластомы):
Новый коэффициент отбора после ослабления его интенсивности равен 16,8% от прежнего (до релаксации) коэффициента отбора (s=l). Частота гетерозигот в (п + 1)-м поколении, Хп + v получается из частоты гетерозигот в n -м поколении, Х п, путем применения следующей приближенной формулы:
Из этой рекуррентной формулы можно получить общую формулу для Хn.
Таким образом, новая равновесная частота гетерозигот X представляет собой сумму членов геометрической прогрессии с начальным членом Хо = 2μ и знаменателем (1 — s 2 ):
Этот результат может быть получен также из уравнения (6.1). Отсюда следует, что через несколько поколений после применения эффективного лечения наследственная ретинобластома станет встречаться примерно в 6 раз чаще. Используя реальные оценки, полученные для современных популяций (см. табл. 5.8), получаем Х0= 2μ = 1,2 х 10–5:
6. Популяционная генетика 299 Из этой величины можно вычислить суммарную частоту всех случаев ретинобластомы, включая ненаследственные случаи, если известна доля наследственных случаев среди всех случаев ретинобластомы в популяции перед ослаблением отбора. Общая частота ретинобластомы приблизительно равна 4 х 10–5; следовательно, около 2,8 х 10–5 – частота наследственной формы. Отсюда получаем оценку равновесной частоты после ослабления отбора: 7,14 х 10–5 + 2,8 х 10–5 = 9,94 х 10–5. Это значит, что частота ретинобластомы возросла с ≈1:25000 до 1:10000, т.е. на 150%. Кроме того, до ослабления отбора наследственными являлись около 30% случаев, тогда как при новом состоянии равновесия наследственными окажутся уже ≈ 72%. Это равновесие устанавливается относительно быстро (рис. 6.9): через 9 поколений частота наследственной ретинобластомы увеличилась более чем в 4 раза по сравнению с соответствующей частотой до ослабления отбора (при равновесии X = 5,95 Х 0 ). На рис. 6.9 приведены также расчеты для двух альтернативных случаев: s2 = 0,4 и s2 = 0, т. е. отбор отсутствует. В последнем случае частота возрастает линейно и равновесие не устанавливается. Можно все же надеяться, что теоретически рассчитанные частоты на станут фактическими, естественный отбор будет частично заменен искусственным, благодаря генетическому консультированию и добровольному контролю над рождаемостью, осуществляемому носителями данной мутации. Отбор путем полной элиминации гомозигот. Гомозиготы по многим рецессивным аутосомным заболеваниям обычно не размножаются. Рассмотрим опять два аллеля А и а, имеющие частоты р и q. Однако пусть теперь против гомозигот аа действует отбор: s=1; w22 = 0. Частота зигот указана в таблице. В общем случае частоты генов в двух последовательных поколениях п и n + 1 связаны следующим образом:
Эта формула выражает рекуррентное соотношение между последовательными частичными суммами (суммами первых п
членов) гармонической последовательности1). Из нее можно получить общую формулу для генной частоты qn через п поколений:
Изменение частоты гена за поколение равно
Из уравнения (6.3) следует, что qn = q 0 /2, если nq 0= 1. Следовательно, через п = 1 /q 0поколений частота гена уменьшится вдвое. Рассмотрим важное практическое при-
1) Гармоническая последовательность – это такая последовательность, последовательные частичные суммы которой являются величинами, обратными соответствующим членам арифметической последовательности:
300 6. Популяционная генетика ложение полученных соотношений. Если размножение гомозигот по кистозному фиброзу будет полностью отсутствовать, как это повлияет на частоту данного гена? Коэффициент отбора против гомозигот s= 1.
Частота гена, определяющего это заболевание, q0 = 0,02, что соответствует частоте гомозигот в панмиктической популяции, равной q02 = 0,0004, т. е. 4 больных на 10000 индивидов. Через п = 1/0,02 = 50 поколений q0 уменьшится с 0,02 до 0,01. Принимая длительность поколения за 30 лет, такое уменьшение частоты гена в два раза потребует 1500 лет. В случае более редких заболеваний, таких, как галактоземия, q0 = 0,005, q2 = 1:40 000; частота гена уменьшится вдвое за 200 поколений, или 6000 лет. Таким образом, попытки снизить число рецессивных генов в популяции путем прекращения репродукции гомозигот крайне неэффективны. Более того, в этих расчетах даже не принимались во внимание вновь возникающие мутации. Частичная элиминация гомозигот. При некоторых рецессивных заболеваниях гомозиготы не теряют репродуктивной способности полностью, однако их биологическая приспособленность сильно понижается. Предположим, что репродуктивная способность гомозигот снизилась на s (1 > s > 0). Частоты генов до и после отбора можно взять из таблицы 6.5. Они дают такую частоту рецессивного аллеля в следующем поколении:
Соотношение между частотами рецессивного аллеля в двух последовательных поколениях задается формулой
Вероятно, эта рекуррентная формула не имеет общего решения. Изменение частоты на поколение равно
Δ q зависит как от qn, так и от рп = 1 — qn. Если одна из этих величин мала, Δ q также мало. Например, для s = 0,2 q: 0,99 0,50 0,01 Δ q: – 0,00244 – 0,0263 – 0,0000198. При очень малых значениях q, Δ q аппроксимируется – sq2. Некоторые расчеты. Для того чтобы определить изменение q за большое число поколений, Δ q можно заменить на
Интегрируя обе части по п поколениям, получаем
Вычисление числа поколений (п), необходимого для того, чтобы q изменилось на определенную величину (при s — 0,01 против гомозигот), дает следующие величины:
6 Популяционная генетика 301 За это время могут произойти события, которые значительно сильнее повлияют на генетический состав популяции. Гаметический отбор. До сих пор мы предполагали, что отбор действует на стадии зиготы. Однако отбор может происходить уже на стадии гаметы. Из-за своего генетического состава некоторые гаметы имеют меньшую вероятность оплодотворения по сравнению с остальными. Если какая-нибудь мутация оказывает влияние на вероятность оплодотворения, по этой мутации будет наблюдаться отклонение от нормального расщепления. Предполагается, что именно этим объясняется аномальное расщепление, наблюдающееся при синдроме Алпорта и оптической атрофии Лебера (разд. 3.1.5). Для всех других заболеваний соответствие с менделевским расщеплением обычно считается очевидным. На самом деле это может быть не так, поскольку для демонстрации незначительных отклонений от менделевских соотношений необходимы большие выборки. Однако возникновение существенных отклонений маловероятно. В случае гамет, несущих сбалансированные и несбалансированные транслокации, нарушение расщепления несомненно имеет место, однако его механизм еще не выяснен (разд. 2.2.2). Если относительный вклад гамет А и а в генофонд следующего поколения составляет 1 и 1 — s, а их частоты равны р и q, то их вклад в генофонд следующего поколения будет р и q( 1 — s) соответственно. Тогда изменение генной частоты на поколение
Все приведенные выше примеры на самом деле не очень просты. Поскольку отбор, вероятно, по-разному действует на зародышевые клетки разного пола, ситуация усложняется в случае таких аномалий, как например, транслокации. С формальной точки зрения, гаметический отбор почти идентичен отбору против гомозигот и гетерозигот с промежуточным значением приспособленности (табл. 6.6).
Дата добавления: 2015-12-16 | Просмотры: 895 | Нарушение авторских прав |


 = μ/s. (6.1)
= μ/s. (6.1)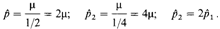
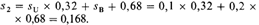
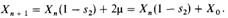

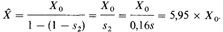
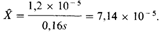
 (6.2)
(6.2)
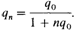 (6.3)
(6.3) (6.4)
(6.4) В данном конкретном случае b = 1; с = k = и0.
В данном конкретном случае b = 1; с = k = и0.


 (6.5)
(6.5)