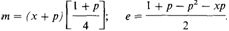|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Другие формулы отбораЧастотно-зависимый отбор [103; 1739]. До сих пор мы считали, что селективные ценности генотипов постоянны. Однако они могут быть функцией частоты генотипов 306 6. Популяционная генетика
или плотности популяции. Такой тип отбора известен как частотно-зависимый. Говоря конкретнее, при отрицательной корреляции между селективной ценностью генотипа и его частотой генотип с уменьшением его частоты становится более селективно ценным. В разд. 3.5.5 в качестве примера неравновесия по сцеплению по тесно сцепленным локусам, обусловленного селективным преимуществом некоторых комбинаций аллелей (гаплотипов), приведена бейтсовская мимикрия у бабочки Papilio memnon. Пример Papilio memnon иллюстрирует также частотно-зависимый отбор: селективная ценность мимикрирующей формы зависит от отношения ее частоты к частоте вида, который она имитирует (модели). Когда мимикрирующая форма имеет низкую частоту, хищники встречают несъедобную модель чаще, чем мимикрирующий вид. Поэтому они начинают избегать и модель, и мимикрирующую форму, что приводит к селективному преимуществу последней. Однако при увеличении частоты мимикрирующей формы хищники будут встречать ее чаще, чем несъедобную модель, и перестанут ее избегать. Если частота мимикрирующей формы намного превысит частоту модели, хищники станут связывать ее внешний вид со съедобностью. Тогда генотип станет селективно невыгодным. Примем следующую простую модель частотно-зависимого отбора по доминантному гену:
Тогда
Следовательно, условие равновесия w 1 = w2 или q2 (s1 + s2) — s1 = 0. Данное уравнение имеет решение относительно частоты гена q тогда и только тогда, когда коэффициенты отбора s1 и s2 оба положительны или оба отрицательны. Это решение имеет вид
Величина приспособленности для соотношения равновесия
Можно показать, что это равновесие стабильно в том случае, когда и s1, и s2 6 Популяционная генетика 307
отрицательны (но не меньше —1). Это значит, что стабильное равновесие существует, если аллель А имеет селективное преимущество при низкой частоте (как в случае бейтсовской мимикрии). В состоянии равновесия приспособленности всех генотипов одинаковы. В отсутствие доминирования, если приспособленности всех трех фенотипов различны, расчеты становятся более трудоемкими [103]. Однако можно показать, что и в этом случае частотно-зависимый отбор приводит к стабильному полиморфизму при отсутствии преимущества гетерозигот. Указанный механизм может поддерживать полиморфизм даже при селективной невыгодности гетерозигот. Более того, в некоторых случаях существует более одной точки устойчивого равновесия. Возможно, что у человека взаимная адаптация паразита к хозяину и наоборот происходит путем частотно-зависимого отбора. Паразит (например, бактерия или вирус) может адаптироваться к наиболее распространенному биохимическому или иммунологическому типу хозяина; при этом более редкие типы будут иметь селективное преимущество [1779]. Паразит имитирует антигены хозяина, либо приобретая способность продуцировать его антигены, либо прямо, используя материал мембраны хозяина для синтеза собственной мембраны. Первый механизм (генетический) реализуют бактерии, содержащие АВН-подобный антиген [211] (разд. 6.2.1.8); второй механизм, возможно, встречается у некоторых вирусов. В обоих случаях иммунные защитные системы хозяина «обмануты» и паразит размножается успешнее, чем в том случае, если бы он не имел общих с хозяином антигенов. Отбор является частотно-зависимым, поскольку вирус в основном адаптируется к наиболее часто встречающемуся генотипу и более редкие генотипы имеют селективное преимущество. Один из способов защиты хозяина от такой «стратегии» паразита – создание им высокополиморфной системы с большим разнообразием сочетаний антигенов на поверхности клеток. В этом случае паразит не сможет получить селективного преимущества, адаптируясь лишь к одному специфическому сочетанию антигенов. Такая высокополиморфная система возникла в случае главного комплекса гистосовместимости (МНС), который включает локусы HLA, а также другие локусы, участвующие в иммунном ответе (разд. 3.5.5). Частотно-зависимый отбор в сочетании с неравновесием по сцеплению [1739]. Отбор может зависеть не только от относительных частот генотипов в популяции, но и от отношения абсолютного размера популяции к размерам ареала, т.е. от плотности популяции. Показано, что сбалансированный полиморфизм поддерживается отбором, зависящим от плотности, в широком диапазоне условий. В определенных обстоятельствах в полиморфной популяции может присутствовать большее число особей, чем в мономорфной. Еще важнее тот факт, что изменения плотности популяции могут привести к генетическим пертурбациям, которые имитируют эффекты генетического дрейфа (разд. 6.4). Изменения популяционной плотности имели большое значение для эволюции человека, например в неолите, когда он осваивал некоторые сельскохозяйственные приемы. Поэтому можно предположить, что отбор, зависящий от плотности, играл большую роль в эволюции нашего вида. Родственный отбор. В последнее время эволюционисты обсуждают другой тип отбора: родственный отбор (или отбор родичей: kin selection). Обычно животные взаимодействуют друг с другом и с окружающей средой, объединяясь в группы: семьи, трибы, стаи. В пределах такой группы часто наблюдается поведение, противоречащее предположению о борьбе каждой особи со всеми другими представителями своего вида за выживание и размножение, т. е. тому, что подразумевалось в ранних моделях отбора. Биологический смысл некоторых форм такого поведения (например, альтруистического), которое иногда даже стоит особи жизни, интуитивно очевиден, скажем, в случае матери, защищающей от хищника свое потомство. Но бывают случаи, когда биологическая основа поведения менее ясна, например лев, «наследующий» гарем, убивает потомство своего предшественника. Теоретическое объяснение такого социального поведения (как альтруистического, так и других типов) оставалось загадкой для эволюционистов со времен Дарвина и до тех пор, пока в 1964 г. 308 6. Популяционная генетика Хамилтон [1784] не разработал теорию родственного отбора. Эта теория сложна и здесь будет рассмотрена только в общих чертах. Однако основная ее идея проста и очевидна: особь борется за сохранение и передачу своих генов. Часто «интересы» генов особи совпадают с ее собственными интересами; однако, к примеру, если особь имеет двух потомков, то, с точки зрения теории, пожертвовать за них жизнью равнозначно спасению своей жизни за их счет, поскольку каждый из них несет половину генов родительской особи. Если потомков трое или больше, альтруистическое поведение приобретает еще большую ценность, так как при выживании потомков сохраняется большее количество генов родительской особи, чем в случае ее собственного выживания. Аналогичные рассуждения применимы к сибсам или более отдаленным родственникам (дедам, бабкам, дядям, племянникам и т.д.). С другой стороны, лев владеет гаремом в течение ограниченного промежутка времени. Он «заинтересован» в том, чтобы за это время оставить как можно большее число потомков. Львицы, выкармливающие детенышей другого самца, не овулируют и не способны к зачатию. Следовательно, в интересах льва убить этих детенышей. На теоретических концепциях Хамилтона и его последователей основывается социобиология – отрасль биологии, приобретающая все большее значение (разд. 7.2.4). Ее выводы стали доступными широкому кругу ученых благодаря дискуссии по поводу «эгоистических генов» и вызвали горячие споры между биологами, философами и социологами. Их понимание требует знания концептуальных предпосылок. Ниже приводится простое формальное обоснование альтруистического поведения [1738]: Ген А обусловливает альтруистическое поведение его носителей. Например, самка дрозда, пролетая очень близко от кошки, отвлекает ее внимание от своих птенцов с риском быть пойманной самой. Альтруистическое поведение может снизить приспособленность особи на величину с, в то же время повышая приспособленность родственной ей особи на величину b. Ген А имеет селективное преимущество, если с/b < r, где r - «коэффициент связи» между донором и реципиентом, r измеряет вероятность того, что копия данного гена донора имеется у реципиента; величина r зависит только от относительного положения донора и реципиента в родословной. В отсутствие инбридинга значения r равны:
Это означает, что r равно доле общих по происхождению генов, которые имеют две особи (см. разд. 6.3.1). Теперь выведем это правило для простой диплоидной модели со следующими характеристиками. 1. Один локус, два аллеля; А – ген «альтруизма» (частота равна р); а - ген «эгоизма» (частота равна q). 2. Популяция панмиктическая, ее численность бесконечно велика. 3. Ген А определяет взаимоотношения между двумя родственными особями, например «сибс—сибс» или «двоюродный сибс—двоюродный сибс». 4. Поскольку предложенное условие распространения гена А – r > с/b, то в модели условие распространения этого гена с/b <?, и? сравнивается с r. Если приспособленности трех генотипов (АА, Аа и аа) равны w11 w12 и w22 соответственно, условие распространения гена аллеля А [45]: р(w11 – w21) + q (w21 – w22) > 0. Приспособленности можно записать следующим образом: w11 = 1 + s, w21 = 1 + r, w22 = 1 + t, где r, s и t обозначают дополнительные изменения приспособленности, происходящие в результате альтруистического поведения. Теперь определим следующие величины: N - размер популяции (очень большой); п - число «альтруистических действий» на поколение; b - приращение приспособленности особи, которой была оказана помощь; с - убыль приспособленности особи, оказавшей помощь; т - доля п действий в помощь индивидам АА; е - доля п действий в помощь индивидам Аа; х - доля п действий, где «помощник» имеет генотип АА. Используя эти определения, можно записать приспособленности следующим образом:
В этих уравнениях генотипам просто придаются коэффициенты, определяющие уменьшение (с) или увеличение (b) их приспособленности за счет альтруистического действия (нормированные на число особей). Подставляя эти выра- 6. Популяционная генетика 309 жения в формулу 6.1, получаем
Конечно, знак < изменяется на обратный, если приспособленность увеличивается за счет реципиента. Для того чтобы показать, что в случае полных сибсов (выражение 6.11) сводится к 1/2, как утверждалось выше, необходимо получить формулы для т, е и х. Они имеют следующий вид [1738]:
Если эти выражения подставить в формулу 6.11, оно сводится к 1/2. Сходные расчеты можно произвести для других степеней родства. Более общую и строгую трактовку читатель найдет, например, в работах Хамилтона. Отбор по мультифакториальным признакам с непрерывным распределением. До сих пор мы рассматривали только отбор по отдельным генам. Однако многие нормальные и аномальные признаки и многие заболевания имеют в популяциях непрерывное распределение и детерминируются некоторым точно не установленным числом генов. В принципе, закономерности теории отбора применимы и к этим признакам. Однако, поскольку такие признаки на фенотипическом уровне пока еще не поддаются генетическому анализу (разд. 3.6), здесь необходимо использовать биометрические методы [63; 65; 124]. Эти методы имеют большое значение для селекции растений и животных. Приведем некоторые закономерности отбора по полигенным признакам: 1) изменение количественного признака в популяции под действием естественного отбора пропорционально величине наследуемости (обсуждение концепции наследуемости см. в разд. 3.6.1.5); 2) ответ признака на отбор зависит от интенсивности отбора (рис. 6.15, А и Б); 3) он также зависит от генетической изменчивости популяции (рис. 6.15). В отсутствие генетической изменчивости отбор неэффективен. На рис. 6.16 показаны последствия искусственного отбора в нескольких поколениях. Среднее значение признака сдвигает-
ся в сторону направления отбора, а генетическая изменчивость уменьшается от поколения к поколению до тех пор, пока отбор становится неэффективным. Мутации, вызывающие слабые, почти неразличимые изменения мультифакториальных систем, вероятно, имеют большое эволюционное значение. Под действием отбора эти мутации приводят к медленным и постепенным сдвигам значений количественных признаков. Один из наследственных признаков, имеющих непрерывное распределение и потому считающихся полигенными, - предрасположенность к таким «мультифакториаль- 310 6. Популяционная генетика ным» болезням, как врожденные пороки развития, многие распространенные патологии или расстройства психики. Изменение давления отбора (например, путем успешного лечения врожденных болезней сердца или шизофрении) приведет к изменению кривой распределения предрасположенности к данному заболеванию и, следовательно, к увеличению частоты его встречаемости. Однако произвести количественную оценку таких изменений трудно. Мы недостаточно хорошо знаем, дает ли мультифакториальная генетическая модель адекватное описание реальной ситуации. 6.2.1.6. Отбор, обусловленный инфекционными болезнями [1831; 211] В предыдущих разделах рассмотрены наиболее важные математические модели отбора и некоторые их практические применения к ситуациям, встречающимся в популяциях человека. Однако мы пока не касались типа отбора, который, возможно, является основным в популяциях человека: отбора, возникающего в результате генетически обусловленных различий в восприимчивости к инфекционным заболеваниям. Отбор в результате инфекционных заболеваний в популяциях прошлого. Естественный отбор особенно эффективен, когда он действует за счет дифференциальной смертности до достижения репродуктивного возраста, т. е в детском и юношеском возрасте. Первые достоверные статистические данные по детской смертности были получены в XVIII в. в Европе [1875]. На рис. 6.17 показана выживаемость детей от рождения до 20-летнего возраста в середине XVIII в. в Пруссии, типичной стране Центральной Европы. Более половины новорожденных не доживали до 20 лет. Приблизительно четверть из них погибала в течение первого года жизни. Каковы были причины ранней смертности7 Статистические данные отвечают на этот вопрос только частично, поскольку не все диагнозы того времени можно соотнести с известными сейчас болезнями. Однако не приходится сомневаться в том, что большинство детей умирало от вирусных и бактериальных инфекционных заболеваний, кишечных инфекций, оспы, туберкулеза и кори. Следовательно, можно априорно предположить, что инфекционные болезни являются селективными факторами. Эндемичные инфекции, воздействующие на каждое поколение, должны быть более селективно эффективными, чем эпидемии, возникающие только эпизодически, такие, например, как чума. Дата добавления: 2015-12-16 | Просмотры: 801 | Нарушение авторских прав |


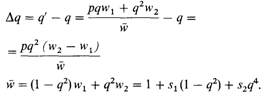

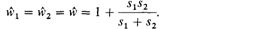
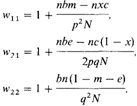
 (6.11)
(6.11)