АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Семейные решения о предложении труда

Выделяются три модели семейных решений о предложении труда:

«шовинистические», в которых доминирующий член семьи принимает решение о предложении труда независимо от других членов семьи, а остальные члены семьи принимают свои решения, рассматривая его заработную плату как часть нетрудового дохода;

предполагающие максимизацию общей семейной функции полезности при наличии семейных бюджетных ограничений;

предполагающие максимизацию индивидуальной полезности при наличии семейных бюджетных ограничений.

В «шовинистических» моделях семейных решений о предложении труда глава семьи независимо от других членов семьи максимизирует свою функцию полезности и находит оптимальное количество часов работы Н_m *:

H * _m = H * _m (w_m / p, V_m / p).

Этому количеству часов работы соответствует доход от трудовой деятельности Y * _m:

Y * _m = (w_m / p) H * _m.

Когда H * и Y * определены, другой супруг максимизирует свою функцию полезности U_f = U_f (C_f, L_f), исходя из решения главы семьи, при этом его бюджетные ограничения будут включать как собственные доходы, так и нетрудовой доход, в который входит собственно нетрудовой доход семьи V_h и заработок главы семьи:

(w_f / p) H_f + [(V_h)+ Y_m) ³ C_f.

В моделях, предполагающих максимизацию семейной функции полезности при наличии семейных бюджетных ограничений, функция полезности имеет вид:

U_h = U_h (C ₁, C ₂,.., C_k, L ₁, L ₂,.., L_n), т. е. максимизируется потребление k различных благ n членами семьи. Если цены на блага остаются в неизменной пропорции, то набор благ можно представить в качестве сложного агрегированного блага СЛ, и функция полезности примет вид:

U_h = U_h (C_h, L₁,.., L_n).

Семейные бюджетные ограничения будут иметь вид:

w_iH_i + V_h ³ C_jp_j,

или с учетом сведения набора потребительских благ в единое агрегированное благо C _h:

(w_i / р) H_i + (V_h / p) ³ C_h, при H_i = Т - L_i.

Решением этой модели будет множество оптимальных часов работы для каждого члена семьи:

H * _i = H * _i (w₁ / р, w₂ / р,.., V_h / p).

Таким образом, количество часов работы каждого члена семьи зависит от ставки реальной заработной платы других членов семьи, цены потребительских благ и нетрудового дохода семьи.

Чем выше заработная плата одного из супругов, тем меньше при прочих равных условиях склонность второго супруга к участию в рабочей силе, поскольку первый имеет сравнительные преимущества на рынке труда. В то же время решение будет зависеть от вида функции полезности. Чем меньшую полезность второй супруг связывает с нерыночной деятельностью, тем более он будет склонен к работе на рынке.

Если внутрисемейный перекрестный эффект замещения равен 0 (т. е. предложение труда никого из членов семьи не зависит от заработной платы других членов семьи), то решение модели примет вид:

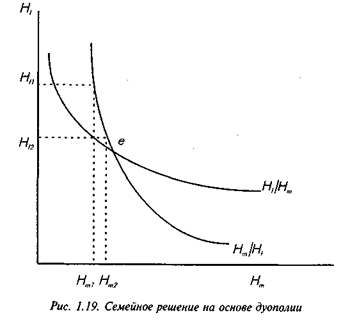
H * _i = H * _i (w₁ / р, V_h / р + (w_g / p) H_g).

В данном случае единственный фактор, при помощи которого другие члены семьи влияют на решение о предложении труда i -го члена семьи — это доход семьи, который теперь образуется из V_h и суммы трудовых доходов других членов семьи (g = 1,.., n; g ¹1).

Модели, предполагающие максимизацию индивидуальных функций полезности при семейных бюджетных ограничениях, подчеркивают роль индивидуума в принятии семейных решений. Эти модели рассматривают максимизацию индивидуальной полезности, когда она является функцией индивидуального досуга и семейного потребления.

Один из вариантов таких моделей основывается на модели дуополии. Кривая реакции первого супруга H_m / H_f и кривая реакции второго супруга H_f / H_m показаны на рис. 1.19. Каждая кривая реакции показывает оптимальный (максимизирующий индивидуальную полезность) выбор количества часов работы данным супругом при определенном количестве часов работы другого супруга. Если второй супруг предлагает H_f1 часов работы, то оптимальным выбором для первого супруга будет H_m1 часов работы. Однако это решение неустойчиво. В ответ на выбор первым супругом количества часов работы H_m1 второй супруг будет оптимизировать свое поведение и выберет H_f2 часов работы. Этот процесс будет продолжаться до тех пор пока решение о выборе часов работы не будет соответствовать точке е на кривых реакции супругов (е — точка пересечения кривых реакции). В данном случае точка е — точка устойчивого равновесия для обоих супругов. Но если наклоны кривых реакции обратны, то точка е не будет точкой устойчивого равновесия. Достаточным условием существования устойчивого равновесия является то, что потребительские блага — нормальные блага для обоих супругов.

Дата добавления: 2016-06-06 | Просмотры: 616 | Нарушение авторских прав