АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Неявные контракты: базовая модель

Из-за экономической конъюнктуры экономика не может оставаться в стабильном состоянии. Заработная плата и прибыль подвержены колебаниям. Можно предположить, что работники различаются по своему отношению к колебаниям заработной платы, т. е. имеют различную склонность к риску потерять часть заработной платы в условиях неопределенности. Работники, не нейтральные к риску, предпочтут стабильную заработную плату. В этом случае трудовые контракты должны включать элементы страхования, защищающие работников в тяжелые времена, когда заработная плата низкая, за счет средств, полученных из недоплаты заработной платы в хорошие времена, когда заработная плата была высокой. Основным положением модели неявных контрактов служит разделение риска между работником и фирмой. «Неявность» контрактов означает, что они имеют неформальный характер, договор между работодателем и работниками не фиксируется письменно. Но отличительной чертой контрактов в данной модели выступает не столько их неявный характер, сколько то, что они фиксируют разделение риска между работниками и фирмой.

Базовая модель неявных контрактов основана на том, что существует конкурентная отрасль, состоящая из одной фирмы, где цена продукта р — случайная переменная, соответствующая величина р ₁ = 1 — а и р ₂ = 1 + а (0 < а <1) при двух состояниях экономики, 1 и 2. Предполагается, что в остальном оба состояния совершенно одинаковы. Существует неэластичное предложение труда N одинаково не приемлющих риск работников в отрасли, их функция полезности u (w + bR), где w — ставка заработной платы, b — ценность досуга (в единицу времени), R — часть времени, отданная досугу (0 < R < 1). Она предполагает, что потребление и досуг являются совершенными заменителями при постоянной предельной норме замещения b. Если w > b, работник будет работать все время (R = 0), а если w < b, все время будет отдано досугу (R = 1). Отсюда следует, что b — резервная цена времени, предложенного для работы на рынке, т. е. резервная заработная плата. Если индивидуум работает, то его полезность задана функцией u (w); если не работает, то полезность равна u (b).

Фирма представлена однофакторной производственной функцией Q = f (L), которая имеет уменьшающуюся отдачу от масштаба. Когда фирма нанимает L (L £ N) работников по заработной плате w и продает свою продукцию по цене р, ее прибыль равна:

p = pf (L) — wL.

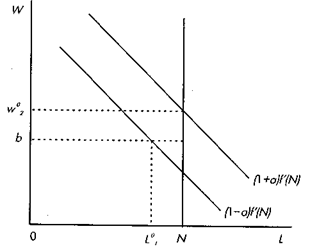
В данном случае предполагается, что фирма нейтральна к риску. Таким образом, она будет заботиться только о максимизации ожидаемой прибыли.

Рисунок 6.7 показывает кривые предельного денежного продукта для каждого из двух состояний экономики. В состоянии 2, когда цена продукта высока, кривая предельного денежного продукта пересекает кривую неэластичного предложения труда N при заработной плате w ⁰₂. В состоянии 1 кривая предельного денежного продукта расположена ниже при предположении, что

(1 - a) f ’(N) < b < (1 + a) f ’(N),

где f ’= ¶ Q/ ¶ L — предельный физический продукт труда.

В состоянии 1 N работников будет занято, только если заработная плата будет меньше резервной заработной платы. Но заработная плата не может быть меньше резервной, поэтому в состоянии 1 w ₁ = b и фирма максимизирует прибыль, нанимая L ⁰₁ работников. Оставшиеся N — L ⁰₁ (работников будут безработными.

Допустим, что фирма и ее работники заключают контракт, в котором до того, как состояние экономики станет известно, они договариваются, что фирма будет платить заработную плату w ⁰₂ и нанимать N рабочих, если возникнет состояние 2, а если возникнет состояние 1, заработная плата будет b, а занятость L ⁰₁. Типичный работник тогда будет иметь определенную

Рис. 6.7. Заработная плата и занятость для двух состояний экономики

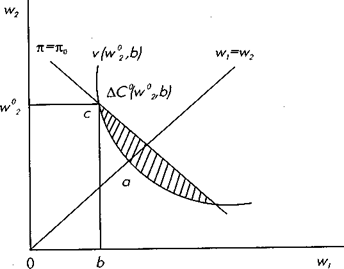
Рис. 6.8. Оптимальный контракт

вероятность оказаться безработным в состоянии 1. Его полезность от пребывания в состоянии занятости и безработицы одинакова: занятым работникам в состоянии 1 платят только их резервную заработную плату, которой хватает только на то, чтобы компенсировать им потерю досуга. Таким образом, возникающая безработица может рассматриваться как добровольная. Обозначим этот контракт как D₀ = (w ⁰₂, b).

На рис. 6.8 этот контракт изображен в пространстве заработных плат для каждого из двух состояний. Предположим, что этот контракт дает фирме ожидаемую прибыль p₀. Так как издержки фирмы могут быть записаны как взвешенная по вероятностям сумма w ₁ и w ₂, изокосты могут быть начерчены в виде линии под углом 45°, где оба состояния могут возникнуть с равной вероятностью. Соответствующая линия изоприбыли может быть представлена прямой линией с наклоном —1, проходящей через точку контракта D₀. Полезность не приемлющих риск работников при данном контракте показана кривой безразличия v (D₀), проведенной через D₀. Если посмотреть на точку а, где зарплата одинакова для обоих состояний, то не приемлющие риск работники примут более низкую заработную плату в состоянии 2 только, если существует непропорциональное увеличение заработной платы в состоянии 1, и наоборот. Из-за предполагаемого неприятия риска работников в точке с наклон будет меньше, чем —1. В общем виде наклон кривой безразличия полезности работника равен — ¶ u /¶ w ₁) / (¶ u /¶ w ₂), соотношению предельных норм замещения заработных плат для двух состояний экономики.

Полезность работника увеличивается в северо-восточном направлении, а прибыль фирмы увеличивается в юго-западном направлении, поэтому все контракты, расположенные внутри площади, ограниченной p₀ и v (D₀), являются, с точки зрения Парето-эффективности лучшими по отношению к D₀. Эффективные по Парето контракты должны лежать на линии определенности работника, где w ₁ = w ₂. Только на линии определенности линия изоприбыли фирмы будет касательной к кривой безразличия полезности работника.

Условие оптимальности контракта будет следующим:

- (¶ u /¶ w ₁) / (¶ u /¶ w ₂) = -1.

Следовательно, оптимальный контракт с точки зрения фирмы при заданной стартовой точке с будет в точке а. Однако в более общем плане при различных стартовых точках все Парето-эффективные контракты лежат вдоль w ₁ = w ₂, так что заработная плата работника не зависит от цены продукта фирмы, т. е. является «жесткой».

Дата добавления: 2016-06-06 | Просмотры: 641 | Нарушение авторских прав