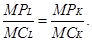|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
В различных по времени периодах производства
Производственную функцию можно представить как:
Q = f (L, K).
Функцию издержек можно определить как:
С = wL + rK.
Решение об объеме спроса на труд, максимизирующем прибыль работодателя, может быть получено с помощью максимизации функции Лагранжа для задачи максимизации выпуска при заданных издержках:
Отсюда следует, что максимизирующее прибыль решение об объеме спроса на труд будет подчиняться условию:
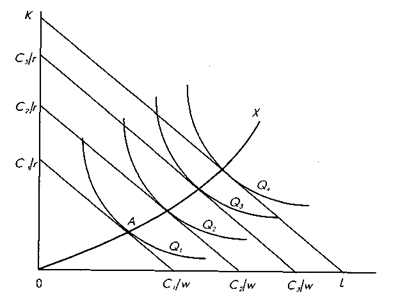
Таким образом, в долгосрочном периоде объем спроса на труд определяется условием равенства отношения предельного продукта труда к предельным издержкам труда и отношения предельного продукта капитала к предельным издержкам капитала. На рис. 2.2 показаны линии изоквант производственных функций Q 1, Q 2, Q 3, Q 4, каждая из которых показывает все возможные комбинации К и L, необходимые для производства определенного количества продукта.
Рис. 2.2. Выбор оптимального соотношения труда и капитала при изменении объема выпуска
Изокванты выпуклы, так как труд и капитал могут замещать друг друга в процессе производства. Диагональные прямые, касательные к изоквантам, — изокосты — показывают фиксированную для каждого случая сумму С, которая может быть потрачена на приобретение факторов производства. Предположим, что стоимость услуг капитала составляет r за единицу, а ставка заработной платы w. Если фирма использует все имеющиеся у нее ресурсы на приобретение капитала, она может купить C 1/ r единиц капитала. Если СI полностью потрачено на труд, можно купить C 1/ w человеко-часов. Величина наклона линии бюджетных ограничений составляет C 1/ r, деленное на C 1/ w, или w / r. Так как изокосты отрицательно наклонены, то угол наклона равен — w / r. Точка касания А показывает положение, минимизирующее издержки производителей в долгосрочном периоде. В этой точке они производят объем продукции Q 1 используя наименее дорогую комбинацию факторов. В точке А касание изокосты и изокванты означает, что углы их наклона равны, или
MPL / MPK = w / r = MRTS,
где MRTS — предельная норма технического замещения, которая показывает, насколько сложно технически заменить один фактор производства другим. Основной закон переменных пропорций для выбора двух факторов производства гласит: факторы будут использоваться так, что относительные объемы производства, добавляемые дополнительной единицей каждого фактора, пропорциональны их относительным стоимостям. При неизменных ценах на факторы производства увеличение общей суммы издержек графически выразится в параллельных сдвигах вверх и вправо линий изокост. Каждая из этих изокост будет касательной только к одной изокванте. Точки касания изоквант и изокост показывают максимальный выпуск продукции при данном уровне затрат или минимальные издержки, необходимые для данного выпуска продукции. Линия, соединяющая все точки касания изокост и изоквант, показывает, как количество используемых факторов производства будет изменяться с изменением уровня выпуска фирмы. Эта кривая называется «путь развития фирмы» и представлена линией 0 Х на рис. 2.2. Таким образом, путь развития фирмы показывает, как меняется спрос на труд в долгосрочном периоде при изменении объема выпуска продукта.
Дата добавления: 2016-06-06 | Просмотры: 835 | Нарушение авторских прав |
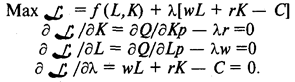
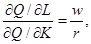 или
или 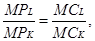 или
или