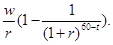|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
В течение жизненного цикла
Воспроизводство человеческого капитала в течение жизненного цикла рассматривается в модели Бен-Пората. В ней предполагается, что в каждый год своей жизни человек инвестирует в себя — покупает единицы человеческого капитала — в соответствии с выгодами и издержками покупки этих единиц на данном этапе человеческого цикла. Выгоды равны текущей стоимости дополнительной заработной платы, которая может быть получена благодаря дополнительной единице профессионального обучения. Издержки — это в первую очередь упущенные заработки, возникающие из-за того, что часть времени направлена на получение дополнительной единицы человеческого капитала. Индивидуальные инвесторы покупают человеческий капитал до того момента, когда предельные издержки становятся равны текущей стоимости предельных выгод. Элементы модели показаны на рис. 4.9. Центральный компонент — это производственная функция человеческого капитала, представленная в квадранте I. Человек может использовать свой человеческий капитал либо для зарабатывания денег на рынке, либо для обучения с целью производства нового человеческого капитала, т. е. фактором производства нового человеческого капитала является имеющийся человеческий капитал, который человек направляет не на получение дохода, а на самоинвестирование. Обозначим этот фактор как stKt, где st — доля запаса человеческого капитала Kt направленная на самоинвестирование. Простая производственная функция человеческого капитала Qt = (stKt) b, где 0 < b < 1 — параметр «способностей». Проблема индивидуального решения заключается в выборе st для каждого периода.
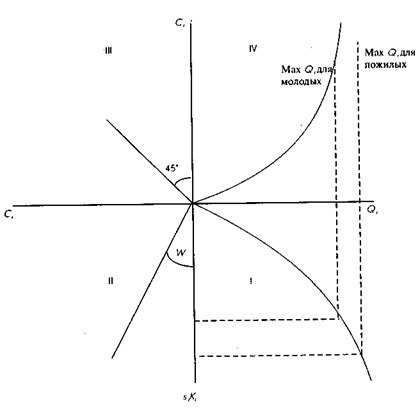
Рис. 4.9. Производственная функция человеческого капитала и функция общих издержек на производство человеческого капитала
Поскольку st не может быть больше единицы, постольку максимум Q, который может быть произведен в каждый данный год t, ограничен существующим запасом капитала, К. Однако так как Kt увеличивается с возрастом (при предположении, что инвестиции продолжаются), максимальный возможный объем производства капитала Q растет с возрастом. Инвестирование в воспроизводство человеческого капитала приводит к издержкам в виде упущенных заработков (возможны и прямые издержки на оплату обучения, но в данном случае мы предполагаем, что они незначительны). Упущенные заработки Ct — это заработная плата на единицу человеческого капитала w, умноженная на количество единиц человеческого капитала, направленных не на работу на рынке, а на самоинвестирование:
Ct = w st Kt. Эта функция изображена в квадранте II. Квадрант III является вспомогательным, в нем проведена линия под углом 45° к началу координат, которая позволяет перенести денежные издержки в квадрант IV, где в результате мы получим функцию общих издержек на производство единиц человеческого капитала. Отметим, что при достижении максимума Qt функция издержек заканчивается (пунктирная вертикальная линия), причем максимум с возрастом сдвигается вправо. Сформулированная таким образом функция производства человеческого капитала основана на использовании только собственных ресурсов индивидуума. Предполагается, что заем средств для самоинвестирования незначителен, и роль семейных средств также незначительна (благосостояние семей может быть отражено в модели через более низкую ставку дисконтирования при оценке выгод от инвестирования). Выгоды от дополнительной единицы человеческого капитала — это текущая стоимость потока будущей заработной платы PV (w, r), которую принесет эта единица. Поток продолжается до выхода на пенсию. Если принять возраст выхода на пенсию равным 60 годам, тогда выгоды Bt равны:
Bt = PV (w, r) Qt,
Bt =
Bt @ Bt @ 0, когда человек приближается к пенсионному возрасту (t @ 0). На рис. 4.10а показан график выгод и уже выведенная функция общих издержек. График выгод — это прямая линия, проведенная из начала
Рис. 4.10. Общие и предельные выгоды и издержки производства человеческого капитала
координат. Наклон ее для молодых работников будет круче, чем для пожилых, потому что текущая стоимость единицы человеческого капитала для молодых рабочих больше. Наклон также будет круче, если ставка дисконтирования r меньше, т. е. если человек может позволить себе ждать. Точка, в которой разность между общими выгодами и издержками, максимальна, показывает максимизирующую прибыль величину производства человеческого капитала. На рис. 4.10б это объем Q 1 для молодого человека. На уровне Q 1 наклон кривых выгод и издержек одинаков, т. е. предельные выгоды равны предельным издержкам, что показано на рис. 4.10б. Так как текущая стоимость единицы человеческого капитала для молодых работников выше, чем для пожилых, оптимальный объем производства человеческого капитала сокращается в течение жизненного цикла. На рис. 4.10а кривая выгод работников старших возрастов расположена ниже, соответственно на рис. 4.10б кривая предельных выгод для работников старших возрастов тоже расположена ниже. Предположив, что кривая предельных издержек с возрастом остается неизменной, получим точки пересечения предельных выгод и предельных издержек. На рис. 4.10б показан объем производства человеческого капитала для молодого человека Q 1 и для пожилого человека Q 2. Из производственной функции человеческого капитала и функции издержек инвестирования следует:
Ct = w Qt 1/ b .
Предельные издержки МС будут равны:
МС = ¶ С /¶ Qt = Предельные выгоды MB будут равны: MB =¶ B /¶ Qt = Из равенства предельных выгод и предельных издержек МС = MB, получаем решение для Qt *:
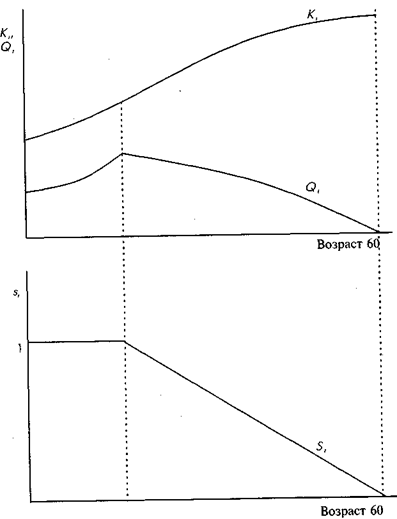
Qt *= [ b / r (1 - 1/ (1 + r)60 - t )] b /(1 - b ). Рассмотрим теперь типичного человека в течение жизни. Предположим, что издержки с возрастом не меняются, только вертикальный участок, показывающий максимум Qt сдвигается с возрастом. В первые годы текущая стоимость выгод от каждой единицы инвестиций относительно велика, а максимум Qt низок, так что индивидуум будет в угловой точке, производя, насколько возможно больше Qt т. е. выбирая долю времени на инвестирование st равную единице, и не оставляя время на работу. С возрастом максимум сдвигается вправо, а кривая предельных выгод сдвигается вниз. В тот год, когда работник выходит на пенсию, кривая предельных выгод пересекает горизонтальную ось координат. На рис. 4.11 показаны кривая инвестиций в человеческий капитал в течение жизненного цикла Qt и соответствующая кривая запаса человеческого
Рис. 4.11. Производство человеческого капитала в течение жизненного цикла
капитала Kt, а также изменение во времени st. Объем инвестиций в человеческий капитал Qt на начальном этапе возрастает, так как в этот момент инвестиции прибыльны, но индивидуум не может производить их в достаточной степени и выбирает st = 1. С возрастом Qt постоянно снижается вплоть до нулевого уровня в возрасте выхода на пенсию. Запас человеческого капитала Kt рассчитывается путем сложения ежегодных инвестиций. Сначала он резко возрастает в период, когда st = 1, затем растет медленнее в среднем возрасте и прекращает расти в пожилом возрасте. Если не учитывать обесценение, запас человеческого капитала достигает пика в возрасте выхода на пенсию и является выпуклой функцией, похожей на профили возраст-заработки. Однако профили возраст-заработки достигают пика несколько раньше пенсионного возраста, а затем имеют наклон вниз. Это происходит потому, что с возрастом некоторые навыки обесцениваются и могут даже оказаться бесполезными, т. е. запас человеческого капитала может разрушаться, причем в старшем возрасте такое разрушение сильнее из-за ухудшения состояния здоровья работника.
Дата добавления: 2016-06-06 | Просмотры: 871 | Нарушение авторских прав |
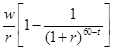 Qt,
Qt,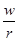 Qt, когда человек молод (t невелико),
Qt, когда человек молод (t невелико),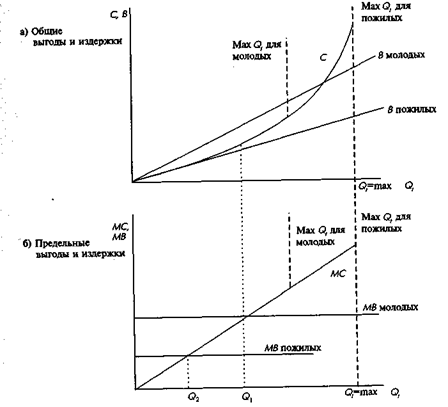
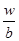 Qt (1- b )/ b
Qt (1- b )/ b