 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Кутові швидкості ланокМЕТОДИЧНІ ВКАЗІВКИ ДО КУРСОВОГО ПРОЕКТУ ПО ДИСЦИПЛІНІ «ТЕОРІЯ МЕХАНІЗМІВ І МАШИН» для студентів спеціальностей 12.01, 17.01
Дніпропетровськ Міністерство освіти і науки України
Національний гірничий університет
МЕТОДИЧНІ ВКАЗІВКИ ДО КУРСОВОГО ПРОЕКТУ ПО ДИСЦИПЛІНІ «ТЕОРІЯ МЕХАНІЗМІВ І МАШИН»
для студентів спеціальностей 12.01, 17.01
Затверджено навчально-методичним управлінням університету
Дніпропетровськ Методичні вказівки до курсового проекту по дисципліні «Теорія механізмів і машин» для студентів фахів 12.01, 17.01 Укл. В.В.Мішин, С.М.Куваєв, О.І.Пучков - Дніпропетровськ: НГАУ, 1997. - с.
Укладачі: В.В.Мішин, д-р техн. наук, професор, С.М.Куваєв, канд. техн. наук, доцент О.І.Пучков, асистент
Відповідальний за випуск С.М.Куваєв, канд. техн. наук, доцент ЗМІСТ
Вступ...…………………………………………………………………… 1. Структурний аналіз механізму...…………………………………… Визначення числа рухливих ланок, класу і числа кінематичних пар, числа ступенів волі механізму...………...………………………………….. Виділення структурних груп і визначення класу механізму...……………………………………………………………. 2. Кінематичний аналіз плоского важільного механізму...………....… 2.1. Побудова плану положень механізму...…………………....…. 2.2. Визначення швидкостей точок ланок механізму...…………... 2.3. Визначення прискорень точок ланок механізму...…………… 2.3.1. Побудова планів прискорень...……………………………. 2.3.2. Кінематичні діаграми...…………………………………….. 3. Динамічний аналіз і синтез плоского важільного механізму...……. Визначення головних векторів сил і моментів інерції, що діють на ланки...………………………………………………....………………. 3.1. Визначення реакцій у кінематичних парах...……………….... Визначення врівноважуючого моменту, прикладеного до вхідної ланки...………………………………………………………………… 3.2. Обчислення приведеного до вхідної ланки моменту сил опору...………………………………………………………….. 3.3. Обчислення приведеного до вхідної ланки моменту інерції... 3.4. Визначення розмірів маховика...……………………………… 4. Синтез кулачного механізму...……………………………………….. 4.1. Вихідні дані для синтезу плоского кулачного механізму...…. 4.2. Формулювання задачі проектування кулачного механізму.… 4.3. Графічне інтегрування кінематичних діаграм штовхальника.. 4.4. Динамічний синтез кулачного механізму...…………………… 4.5. Кінематичний синтез кулачного механізму...……………….... 5. Геометричний синтез прямозубчатого зовнішнього зачеплення...… 5.1. Задача синтезу...………………………………………………… 5.2. Визначення розмірів зубцюватого зачеплення...……………… Порядок креслення елементів зубцюватого зачеплення, дуг зачеплення і робочих ділянок профілів зубів...…………………………………….. 5.3. Визначення якісних показників зачеплення...………………… 6. Проектування кінематичної схеми планетарного редуктора...……... 6.1. Визначення передатного числа зубцюватого механізму...……………....……………………………………… 6.2. Вибір чисел зубів коліс і числа сателітів...…………………… 7. Зміст графічної частини проекту...…………………………………..... 8. Список літератури...……………………………………………………. 9. Додатки...……………………………………………………………….. ВСТУП
Курсовий проект по навчальній дисципліні "Теорія механізмів і машин" є підсумковою роботою в механіко-математичній підготовці студентів, що закріплює їхню теоретичну підготовці по циклумеханічних дисциплін. Він побудований на основних положеннях «Вищої математики», «Теоретичної механіки» і «Теорії механізмів і машин». Ціль проекту – на прикладі конкретного механізму вирішити задачі аналізу та синтезу. Поставлена ціль досягається рішенням за допомогою розрахунково-графічних методів ТММ задач структурного, кінематичного і динамічного аналізу плоского важільного механізму і задач синтезу кулачного і зубцюватого механізму. Курсовий проект закріплює звички студентів по оволодінню загальними методами дослідження і проектування машин і механізмів, розуміння загальних принципів реалізації руху за допомогою механізмів, взаємодії механізмів в машині, дозволяє здійснити системний підхід до проектування механізмів і машин, визначення оптимальних параметрів механізму при заданих параметрах режиму роботи. Курсовий проект складається з розрахунково-пояснювальної записки (написаної рукописно на листах формату А4, яка містить: зміст, введення, структурні, кінематичні, динамічний аналізи плоского важільного механізму, синтез кулачкового і зубцюватого механізму, список використаної літератури) і графічної частини на п’ятьох листах формату А1. Розрахунково-пояснювальну записку і графічну частину проекту виконують відповідно до вимог ЄСКД. 1. СТРУКТУРНИЙ АНАЛІЗ ПЛОСКОГО ВАЖІЛЬНОГО МЕХАНІЗМУ
(Цей розділ студент виконує або в пояснювальній записці, або на першому листі, де поданий кінематичний аналіз.)
Задача аналізу: визначення числа рухливих ланок; класу і числа кінематичних пар, числа і класу структурних груп, класу механізму і його числа ступенів свободи.
1.1 Визначення числа рухливих ланок, числа і класу кінематичних пар, числа ступенів свободи механізму. На малюнку, приміщеному в пояснювальній записці, повинна бути подана схема плоского важільного механізму, накреслена в довільному масштабі, на якій нумеруються рухливі ланки і заголовними буквами латинського алфавіту позначаються кінематичні пари. Студент визначає клас кінематичних пар і для кінематичних пар п’ятого класу встановлює їхній вид: обертальна або поступальна кінематична пара. Результати аналізу відображаються в пояснювальній записці. Число ступенів свободи для механізму визначається по формулі П.Л.Чебишева
W = 3n – 2p5 – p4 (1.1)
де: n – число рухливих ланок механізму; p5 – кількість кінематичних пар п’ятого класу; p4 – кількість кінематичних пар четвертого класу. Якщо в результаті розрахунку ступень рухливості механізму виявиться відмінною від одиниці (W ¹ 1), то варто провести пошуки ланок, що визначають наявність пасивних зв’язків і зайвих ступенів свободи. При виявленні таких ланок їх варто виключити зі структурної схеми механізму, накреслити отриману при цьому нову структурну схему і визначити число ступенів свободи механізму.
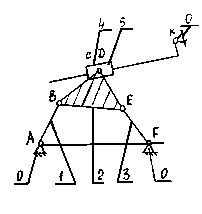
1.2. Виділення структурних груп (СГ) і визначення класу механізму Для визначення класу механізму необхідно “позбутися” від кінематичних пар 1V-го класу (якщо вони є в аналізованому механізмі, замінивши їх на одну ланку з двома кінематичними парами V-го класу. Накреслити отриману при цьому структурну схему даного механізму. Як відомо, складні механізми можуть бути отримані методом нашарування, тобто шляхом приєднання до механізму 1-го класу (по вхідній ланки) структурних груп (груп Асура). Таким чином, при аналізі складного механізму він може бути розділений на СГ і механізм 1-го класу. При цьому клас механізму визначається структурною групою найвищого класу, що входить у цей механізм. Виділення структурних груп варто починати з пошуку найбільше віддаленої від вхідної ланки СГ (пов’язаної з вихідною ланкою) 2-го класу з указівкою її виду (модифікації) і порядку. При неможливості виділення (без порушення нерозривності і рухливості механізму) СГ 2-го класу виконують пошук СГ більш високих класів, визначають їхній вид і порядок. Після відділення СГ кінематичний ланцюг, що залишився, повинен являти собою механізм із тим же числом ступенів свободи, що і вихідний. Відділення СГ 2-го і більш високих класів здійснюють до одержання механізму 1-го класу. Всі відділені СГ і механізм 1-го класу повинні бути подані їхніми структурними схемами з указівкою класу і порядку СГ. Механізму присвоюється найвищий клас із виділених СГ. Приклад: виконати структурний аналіз механізму, поданого нижче
Поданий механізм складається із шести ланок, п’ять із яких – рухливі (n = 5). Ланки сполучені між собою сьома кінематичними парами п’ятого класу (p5 = 7): шістьма обертальними – А (0-1), В (1-2), С (2-4), Е (2-3), F (3-0), D (5-0) і однією поступальною D (4-5); КП четвертого класу відсутні p4 = 0. Визначаємо число ступенів свободи механізму:
W = 3n – (2p5 + p4) = 3·5 – (2·7 + 0) = 1.
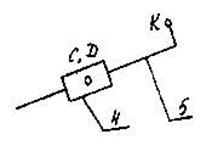
Виділення структурних груп починаємо з найбільше віддаленої від першої (вхідної) ланки СГ 2-го класу третього виду (ВПВ), що складається з ланок 4 і 5 із кінематичними парами С, D, K:
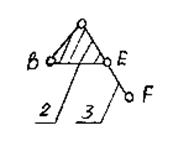
Що залишився після виділення СГ замкнутий кінематичний ланцюг ABEFA являє собою шарнірний чотирьохланковий механізм, для котрого n = 3, p5 = 4 (А, В, Е, F), p4 = 0, а число ступенів свободи W = 3·3 – 2·4 = 1. З цього механізму виділяємо СГ 2-го класу першого виду (ВВВ), що складається з ланок 2 і 3 із кінематичними парами
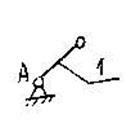
У результаті послідовного відділення двох СГ 2-го класу одержуємо механізм 1-го класу:
Таким чином, вихідний механізм – механізм 2-го класу.
2. КІНЕМАТИЧНИЙ АНАЛІЗ ПЛОСКОГО ВАЖІЛЬНОГО МЕХАНІЗМУ
Розрахункова частина і результати у виді таблиць виконуються в пояснювальній записці, а геометричні побудови, що відносяться до плану положень механізму, планам швидкостей, прискорень, діаграми переміщень, швидкості і прискорення вихідної ланки – на листах.
Задача аналізу: побудова планів положень механізму (включаючи мертві положення) по 12-ти положеннях вхідної ланки важільного механізму, визначення методом плану швидкостей для цих положень механізму лінійних швидкостей вузлових (характерних) точок механізму і кутових швидкостей ланок, побудова по планах положень і швидкостей кінематичних діаграм переміщення, швидкості і прискорення вихідної ланки, графік прискорення вихідної ланки будують методом диференціювання діаграми його швидкості.
2.1.Побудова плану положень механізму План положень механізму будують методом зарубок. Для цього приймається визначене значення масштабного коефіцієнта довжини
де l 1 – довжина вхідної ланки, м, [ l 1 ] – довжина відрізка, що зображує вхідну ланку на кресленні. Для зручності користування масштабним коефіцієнтом розмір відрізка [ l 1 ] може прийматися кратним його фізичній довжині l 1. Обчисляють розміри відрізків [ l і ], що відповідають довжинам l і “і” ланок механізму:
Чисельне значення масштабного коефіцієнта довжини повинно бути вибрано таким, щоб зображуваний план положень не був ні занадто дрібним, ні занадто значним, наприклад, щоб план положень займав приблизно А3 формат у лівій стороні верхньої частини листа формату А1. Чисельне значення масштабного коефіцієнта довжини повинно бути узгоджене з кращими рядами чисел і знаходитися в межах Визначають на кресленні положення нерухомих ланок – стійок (наприклад, А, В та ін.) і будують траєкторії руху вузлових точок ланок, пов’язаних із стійками, прямі лінії для поступальних кінематичних пар і окружності радіусом [ l і ] – для точок ланок, що обертаються навколо стійок. Для траєкторії точки В вхідної ланки (кривошипа), пов’язаної зі структурною групою, що прилежить до нього, задають 12 дискретних, рівновіддалених друг від друга положень, розділивши окружність радіуса, рівного відрізку, зображуючого довжину кривошипа lАВ, на 12 рівних частин. Потім з отриманих 12 точок методом зарубок визначаються положення характерних точок другої і наступних ланок механізму, з’єднання яких для кожного положення кривошипа (у відповідності зі структурною схемою механізму) дозволяє одержати 12 положень важільного механізму. Характерні точки (як правило кінематичні пари) позначають заголовними буквами з цифровими індексами, що відповідають точці розбивки траєкторії вхідної ланки в напрямку його прямування. Мертві положення механізму – положення механізму, у яких швидкість вихідної ланки, змінюючи знак, дорівнює нулю. Для визначення мертвих положень механізму будують шатунну криву (траєкторію руху) точки підєднання структурної групи вихідної ланки. На цій кривій зарубками, виконаними з траєкторії руху вихідної ланки, визначають точки, що відповідають крайнім (мертвим) положенням вихідної ланки.
2.2. Визначення швидкостей точок ланок механізму
Загальні відомості Як відомо, швидкості двох точок N і М, що належать одній ланки, що чинить складне прямування (мал.2.1), пов’язані між собою векторним рівнянням
де - переносна швидкість точки М, VNM - відносна швидкість ланки MN (NM). Причому, у залежності від виду кінематичної пари, у котрій аналізовану ланку пов'язано з прилягаючою до неї в точці N іншою ланкою, відносна швидкість
а напрямок - напрямком вектора відносної швидкості
Плани швидкості ланок механізму
Мал. 2.1 а - при плоскопараллельному руху ланки NM; б - при поступальному русі ланки N;
План швидкості вхідної ланки
Мал. 2.2 Побудова планів швидкостей механізму. починається з нанесення на лист полюса швидкостей Pv (довільна, нерухома точка) із вказівкою індексу, що відповідає положенню механізму, і запису в ньому через коми позначень нерухомих точок, у тому числі стійок. Точки на планах швидкостей і положень позначаються відповідно тими самими прописними буквами латинського алфавіту. Після цього визначається розмір швидкості точки В вхідної ланки (мал.2.2):
де - довжина кривошипа, що обертається навколо стійки А з числом оборотів n1, об/хв; Для побудови вектора швидкості Для зручності користування масштабним коефіцієнтом швидкості
розмір відрізка [ab] рекомендується вибирати кратним розміру швидкості
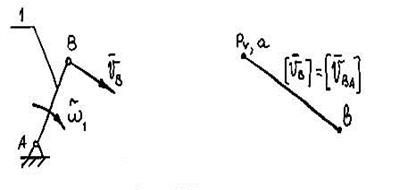
Плани швидкостей структурних груп
Мал. 2.3
а. - СГ 1-го виду (ВВВ); б - СГ 11-го виду (ВВП); в - СГ 111-го виду (ВПВ).
Наступною визначають швидкість точки С, що належить двом ланкам (мал. 2.3) і утворюючу або обертальну, або поступальну кінематичну пару. У цих випадках швидкості зовнішніх кінематичних пар або їхніх елементів повинні бути відомі. Швидкість точки на плані швидкостей визначають графоаналітично у відповідності з рівняннями
в яких двома лініями підкреслені відомі (по розмірі і напрямку) швидкості, а однією лінією - швидкості, для котрих відомий тільки напрямок (перпендикулярно ланки - для обертальних КП, паралельно ланки - для поступальних КП). Перетинання ліній дії відносних швидкостей
де – відрізок [Pvc], який зображує швидкість Одночасно, по довжинах відрізків [bc] і [cd] визначаються розміри відносних швидкостей
Напрямки швидкостей Знаходження швидкостей інших точок, що належать розглянутим вище ланкам, роблять по теоремі подоби, відповідно до якого відношення двох будь-яких відрізків ланки дорівнює відношенню відповідних відрізків плану швидкостей цієї ланки, подібно самій ланки. Побудова планів швидкостей і визначення розмірів швидкостей точок ланок структурних груп, послідовно під’єднаних до ланки найпростішого механізму, для точок якого швидкості уже визначені, виконують по розглянутій вище методиці. Кутові швидкості ланок механізму, що беруть участь у плоскопаралельному або обертальному русі, визначають по залежності (2.4). Побудова плану швидкостей і визначення їхніх розмірів і значень кутових швидкостей роблять для всіх постійних положень механізму. Результати розрахунку швидкостей точок ланок механізму, у тому числі і відносних, заносять у таблиці, де i - номер положення механізму, j - номер ланки механізму, А, В... - кінематичні пари.
Таблиця 2.1 Абсолютні швидкості точок ланок
Таблиця 2.2 Відносні швидкості точок ланок
Таблиця 2.3. Кутові швидкості ланок
2.3. Визначення прискорень точок ланок механізму
Загальні відомості. Як відомо, прискорення точок ланок механізму можуть бути визначені двома методами: методом планів прискорень - для всіх точок механізму в однім положенні механізму і за допомогою кінематичних діаграм - для однієї точки механізму при різноманітних положеннях механізму. У даному проекті методом планів обмежуються при визначенні прискорення точок ланок механізму для трьох його положень. Плани прискорень використовують при динамічному аналізі плоского важільного механізму і будують їх на другому листі. Методом кінематичних діаграм визначають прискорення вихідної ланки для всіх розглянутих раніше положень механізму. 2.3.1 Побудова планів прискорень а) Загальні відомості Як відомо [2], прискорення двох точок M і N ланки, що бере участь у плоскому русі, пов'язані між собою векторним рівнянням:
де У залежності від виду кінематичної пари, яку аналізована ланка утворить із з'єднуємою з нею у точці N іншою ланкою, вектор відносного прискорення для обертальної КП (мал.2.4а)
для поступальної КП (мал.2.4 б)
де Нормальну складову відносного прискорення, направлену по ланки від точки N до точки M, якщо центром обертання прийнята точка M, обчисляють по формулі
Тангенціальну складову відносного прискорення, направлену перпендикулярно ланки NM й указуючу напрямок кутового прискорення
Плани прискорень ланок механізму
а - при плоскопаралельному русі ланки MN; Мал. 2.4 в - при поступальному русі ланки N. Релятивну складову відносного прискорення, направлену по руху ланки по направляючий, визначають із плану прискорень, а кориолісове прискорення ланки знаходять по формулі
де Для визначення напрямку кориолісова прискорення необхідно вектор відносної швидкості
б) Порядок побудови плану прискорень (мал. 2.5, 2.6) Побудову плану прискорень для одного з положень починають із нанесення на лист полюса прискорень Ра (довільна, нерухома точка з прискоренням рівним нулю) із вказівкою індексу, що відповідає положенню механізму, і запису в ньому через коми позначень нерухомих точок, у тому числі стійок. Точки на планах прискорень позначаються також, як і на планах швидкостей прописними буквами латинського алфавіту. Після цього визначають розмір прискорення точки В вхідної ланки
При цьому варто врахувати, що Для побудови вектора прискорення
План прискорень вхідного валу
Мал. 2.5
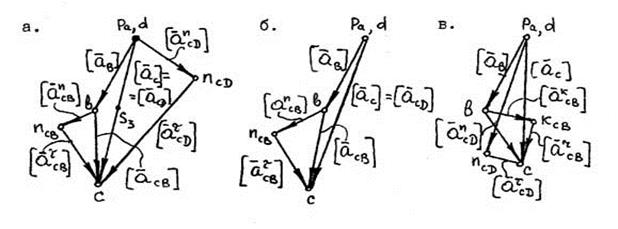
План прискорень структурних груп
Мал. 2.6 а - СГ 1-го виду (ВВВ); б - СГ 11-го виду (ВВП); в - СГ 111-го виду (ВПВ).
Задаються масштабним коефіцієнтом прискорень або вибирають його в масштабі кривошипа. Для зручності користування масштабним коефіцієнтом прискорення Далі визначають прискорення точки С, що належить двом ланкам (мал. 2.3), пов'язаним іншими своїми точками з вхідною ланкою (як правило в точці В) і іншою ланкою (наприклад, із стійкою) прискорення якийсь його точки D відомо. Положення точки С на плані прискорень визначають графоаналітично відповідно до рівнянь: - для обертальних кінематичних пар (мал. 2.3 а):
- коли кінематичні пари В и C - обертальні, а кінематична пара D - поступальна (ланка 3 - камінь) рухається по нерухомій направляючій (мал. 2.3 б):
- для кулісного механізму, коли кінематичні пари В и D - обертальні, а кінематична пара С - поступальна (мал. 2.3 в)
У цих рівняннях однією лінією підкреслені прискорення, для котрих відомо тільки їхній напрямок (
направлені паралельно ланкам СВ і СD відповідно від точки С к точкам В ( Кориолісове прискорення обчислюють по формулі
а його напрямок визначають поворотом на 900 вектора відносної швидкості Для визначення положення точки С на плані прискорень обчислюють розміри відрізків Перетинання напрямків тангенціальних складових (
де [Pac] - відрізок, що зображує прискорення Одночасно, по довжинах відрізків [bc]; [cd]; [nCBc]; [nCDc]; [kCBc] визначають розміри відносних прискорень aCB; aCD:
та їх складових:
Напрямок абсолютного прискорення аС і його складових ( Знаходження прискорень інших точок, що належать раніше розглянутим ланкам, роблять по теоремі подоби, відповідно до якої відношення двох будь-яких відрізків ланки дорівнює відношенню відповідних відрізків на плані прискорень цієї ланки, подібного самій ланки. Для ланок, що рухаються плоскопаралельно або обертально, обчислюють розмір кутового прискорення за допомогою формул
(2.25)
Напрямок кутового прискорення визначають по напрямку вектора Побудова плану прискорень, визначення розмірів і напрямків прискорень точок ланок і структурних груп, послідовно під’єднаних до ланок найпростішого механізму, для точок котрого прискорення вже знайдені, виконують в описаній раніше послідовності. Кутові прискорення ланок механізму, що беруть участь у плоскопаралельному русі, визначають по залежностях (2.25). Результати розрахунку прискорень усіх точок ланок, у тому числі відносних і кутових для трьох положень зводять у таблиці, у яких i - номер положення механізму, j - номер ланки, А, В... - кінематичні пари.
Таблиця 2.4 Дата добавления: 2015-11-26 | Просмотры: 1494 | Нарушение авторских прав |
 (2.1)
(2.1) (2.2)
(2.2)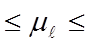
 (2.3)
(2.3) направлена або перпендикулярно (обертальна КП) траєкторії рух ланки MN, або паралельно (поступальна КП). Вектор відносної швидкості на плані
направлена або перпендикулярно (обертальна КП) траєкторії рух ланки MN, або паралельно (поступальна КП). Вектор відносної швидкості на плані  . При плоскопаралельному русі ланки MN (мал.2.1 а) розмір його кутовій швидкості визначається залежністю:
. При плоскопаралельному русі ланки MN (мал.2.1 а) розмір його кутовій швидкості визначається залежністю: (2.4)
(2.4)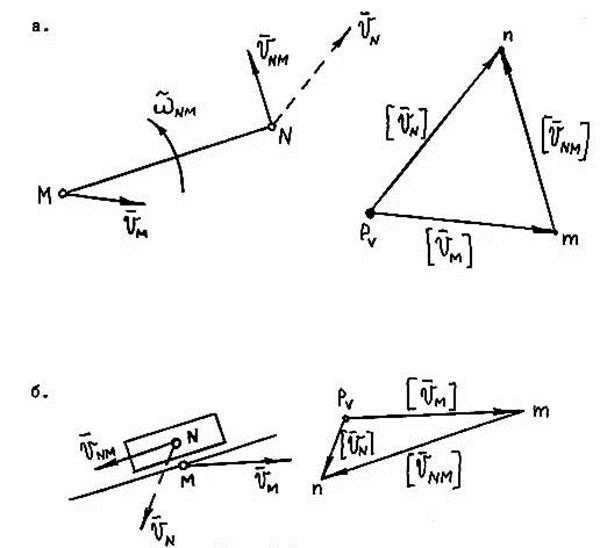
 (2.5)
(2.5) - кутова швидкість кривошипа.
- кутова швидкість кривошипа. 
 через полюс швидкостей проводять лінію перпендикулярну положенню вхідної ланки на плані положень механізму і на ній від полюса в напрямку обертання кривошипа відкладають відрізок [ab], що відповідає значенню швидкості.
через полюс швидкостей проводять лінію перпендикулярну положенню вхідної ланки на плані положень механізму і на ній від полюса в напрямку обертання кривошипа відкладають відрізок [ab], що відповідає значенню швидкості. (2.6)
(2.6) варто узгодити з рекомендованими значеннями масштабів.
варто узгодити з рекомендованими значеннями масштабів.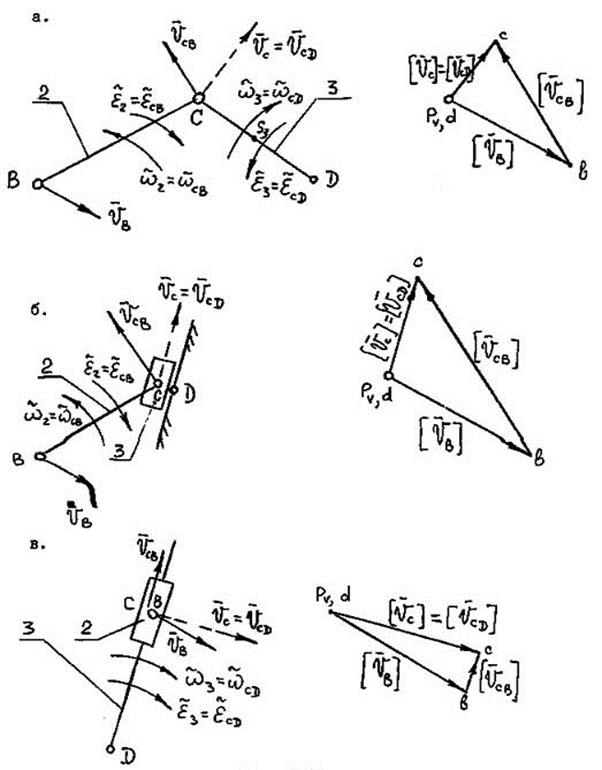
 }
}  (2.7)
(2.7) і
і 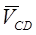 проведених відповідно через кінці векторів і визначить точку С на плані швидкостей і розмір абсолютної швидкості
проведених відповідно через кінці векторів і визначить точку С на плані швидкостей і розмір абсолютної швидкості 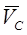 точки С, чисельне значення якої обчислюють по формулі:
точки С, чисельне значення якої обчислюють по формулі: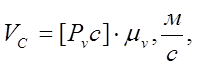 (2.8)
(2.8) (2.9)
(2.9)
 (2.10)
(2.10) - вектор відносного прискорення ланки.
- вектор відносного прискорення ланки. (2.11)
(2.11) (2.12)
(2.12) і
і  - нормальна і тангенціальна складові вектора відносного прискорення,
- нормальна і тангенціальна складові вектора відносного прискорення,  і
і 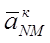 - релятивна і кориолісова складові вектора відносного прискорення.
- релятивна і кориолісова складові вектора відносного прискорення. (2.13)
(2.13) ланки, обчисляють по формулі
ланки, обчисляють по формулі (2.14)
(2.14)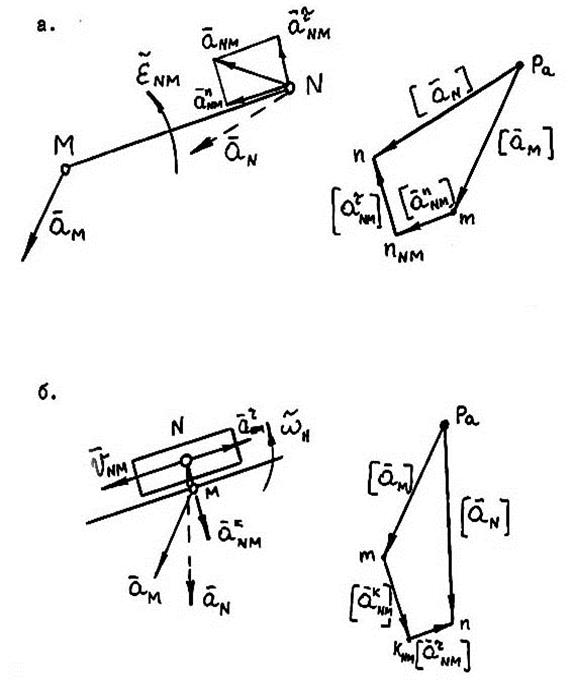
 , (2.15)
, (2.15) - кутова швидкість ланки, по якій рухається повзун.
- кутова швидкість ланки, по якій рухається повзун. (мал.2.1 б) на плані швидкостей для відповідного положення механізму повернути на кут 900 по напрямку обертання ланки-направляючої (по напрямку кутової швидкості
(мал.2.1 б) на плані швидкостей для відповідного положення механізму повернути на кут 900 по напрямку обертання ланки-направляючої (по напрямку кутової швидкості  (2.16)
(2.16) = 0 (при
= 0 (при  ).
). через полюс прискорень проводять лінію паралельно положенню вхідної ланки на плані положень механізму і на ній від полюса в напрямку від точки до стійки А відкладають відрізок [ab], відповідний значенню прискорення
через полюс прискорень проводять лінію паралельно положенню вхідної ланки на плані положень механізму і на ній від полюса в напрямку від точки до стійки А відкладають відрізок [ab], відповідний значенню прискорення 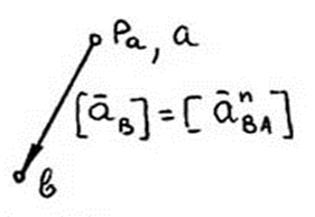
 розмір відрізка [ab] рекомендується вибирати кратному розміру прискорення
розмір відрізка [ab] рекомендується вибирати кратному розміру прискорення  }
}  (2.17)
(2.17) }
}  (2.18)
(2.18) }
}  (2.19)
(2.19) і
і 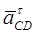 направлені перпендикулярно ланкам СВ і CD;
направлені перпендикулярно ланкам СВ і CD; 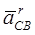 і
і  - паралельно тим же ланкам), а двома лініями - прискорення, для яких відомий напрямок і розмір:
- паралельно тим же ланкам), а двома лініями - прискорення, для яких відомий напрямок і розмір: (2.20)
(2.20) ) і D (
) і D ( ) (мал. 2.6 а, в).
) (мал. 2.6 а, в). (2.21)
(2.21) ланки СВ по напрямку кутової швидкості
ланки СВ по напрямку кутової швидкості 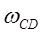 ланки СD (мал. 2.6 в).
ланки СD (мал. 2.6 в). а
а  /mа;
/mа;  =а
=а  /ma; [bkCB]=
/ma; [bkCB]=  і відкладають їх відповідно до вказівок до формул (2.20) і (2.21) від кінців векторів
і відкладають їх відповідно до вказівок до формул (2.20) і (2.21) від кінців векторів  (мал.2.6) та
(мал.2.6) та  .
. і
і  ) прискорень для ланок (мал. 2.3 а), тангенціальної (
) прискорень для ланок (мал. 2.3 а), тангенціальної (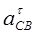 ) і релятивної (
) і релятивної ( ) складових (для ланок мал.
) складових (для ланок мал. 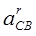 ) і тангенціальної (
) і тангенціальної ( і
і 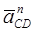 (для ланок мал. 2.3 а),
(для ланок мал. 2.3 а), 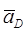 (для ланок мал. 2.3 б),
(для ланок мал. 2.3 б),  і
і  точки С (шляхом побудови вектора, що з'єднує полюс Ра з точкою С на плані прискорень)
точки С (шляхом побудови вектора, що з'єднує полюс Ра з точкою С на плані прискорень) м/с2 (2.22)
м/с2 (2.22) (2.23)
(2.23) (2.23)
(2.23)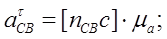
 (2.24)
(2.24)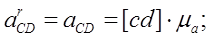
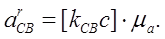
 ;
; 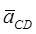 ;
;  ;
;  ;
;  ) визначають по кінцях їхніх векторів, що сходяться в точці С (мал. 2.6).
) визначають по кінцях їхніх векторів, що сходяться в точці С (мал. 2.6). 1/м2;
1/м2; 1/м2.
1/м2. або
або  , умовно перенесеного з плану прискорень на план положення відповідної ланки (СВ або СД) у точку С (при умовно нерухомій точці В (Д)).
, умовно перенесеного з плану прискорень на план положення відповідної ланки (СВ або СД) у точку С (при умовно нерухомій точці В (Д)).