 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Графічне інтегрування функції
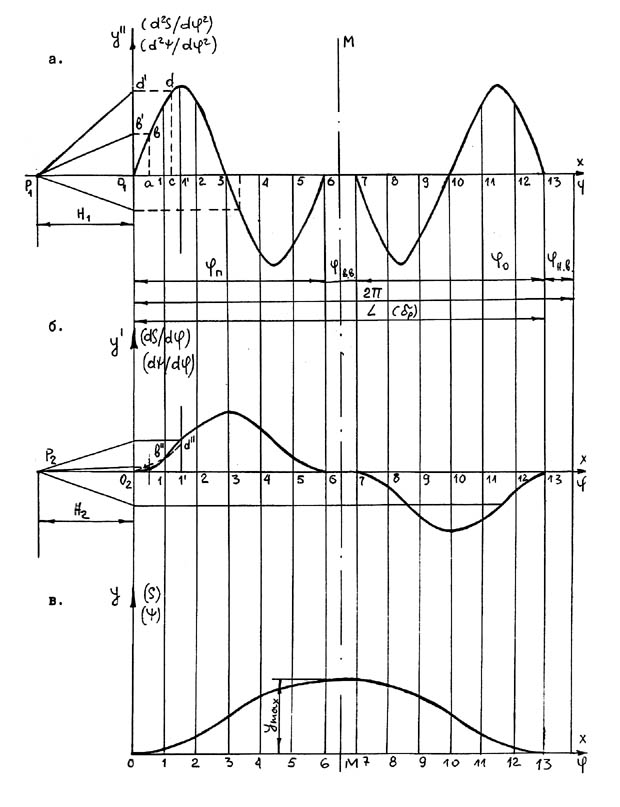
Мал. 4.3 а – первісна функція; б і в – послідовно інтегруємі функції.
Вибір масштабних коефіцієнтів при графічному інтегруванні роблять такою уявою. З огляду на, що при синтезі кулачкового механізму, вісь абсцис Х відповідає рогові повороту кулачка j, а вісь ординат - первісної (мал.4.3 а) - прискоренню вихідного елемента (d2S/dj2) або (dj2) (без указівки масштабів, у яких побудована задана крива), необхідно визначитися з масштабними коефіцієнтами функції й аргументу на графіках (мал.4.3). По осі абсцис X, як правило, відкладають відрізок довжиною L, мм, що відповідає рогові робочого профілю dp на кулачку. У цьому випадку масштабний коефіцієнт (mj(mC)) рогів повороту визначиться залежністю
mx=mj= де довжину відрізка L вибирають, як правило, пропорційної кроку розбивки DX осі абсцис. Відомо [ 2 ], що між масштабними коефіцієнтами діаграм при графічному інтегруванні існують такі залежності (мал. 4.3)
mу=Н2×mх×m (4.3) m де -mу=ms; m При побудові вихідної функції - відрізок L - від 240 мм до 360 мм; - відрізок, що відповідає максимальному значенню - відрізки Н1 і Н2, що визначають положення полюсів Р1 і Р2 у межах 40-60 мм. - Таким чином, задавшись розмірами відрізків L, ( mj= (4.4) m
- або для кулачкового механізму з хитним коромислом: mj= m Знаючи масштаби всіх кінематичних діаграм, визначають значення: пройденого шляху штовхача S=ms-у або рогу повороту коромисла y=mj×у - швидкості штовхача - або коромисла
в будь-якому положенні механізму. Ці значення вписують потім у таблицю 4.1.
Таблиця 4.1
Значення переміщень і рогів повороту і їх похідних
4.4 Динамічний аналіз кулачкового механізму
а) Кулачковий механізм із штовхачем, що зворотно-поступально рухається, (мал.4.1 а)
Для визначення теоретичного початкового радіуса кулачка будують фазовий портрет S- OR=
який розмічають від О точками А1... А13 відповідно до графіка S-j на мал. 4.3 в. Через точки А1, А2.Аі відрізка OR проводять перпендикуляри до нього (горизонталі), на яких відкладають відрізки A1L1, A2L2... AіLі, що відповідають значенням передатної функції (аналогу швидкості (
AіLі=
де масштабний коефіцієнт m
m
Побудову виконують у правій системі координат. При видаленні штовхача передатну функцію (аналог швидкості
[e]=
і точка O1 перетинання цієї лінії з дотичної HM визначить найменший для заданих умов теоретичний радіус ro кулачка ro=O1O×ms (4.14)
Дата добавления: 2015-11-26 | Просмотры: 567 | Нарушение авторских прав |
 ,
,  (4.2)
(4.2)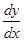
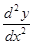
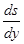 ; m
; m  =m
=m 
 - масштабні коефіцієнти переміщення, аналогів швидкості і прискорення штовхача для кулачкового механізму зі штовхачем, що зворотно-поступально рухаються; - масштабні коефіцієнти рогу повороту, аналогів швидкості і прискорення коромисла для кулачкового механізму з хитним коромислом.
- масштабні коефіцієнти переміщення, аналогів швидкості і прискорення штовхача для кулачкового механізму зі штовхачем, що зворотно-поступально рухаються; - масштабні коефіцієнти рогу повороту, аналогів швидкості і прискорення коромисла для кулачкового механізму з хитним коромислом.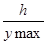 ;
; 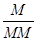 .
.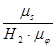 ;
; 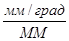 ; m
; m  ;
; 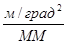
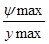 ;
;  =
=  ;
; 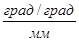 ; m
; m  =
=  . (4.5)
. (4.5)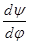 =m
=m 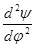
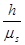 (4.9)
(4.9) (4.10)
(4.10) (4.13)
(4.13)