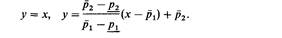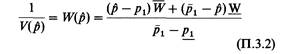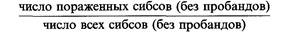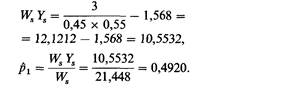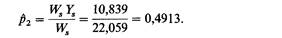|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология
|
Приложение 3 189
| и (s — l)p+1 (для единичного отбора, k = 0) с помощью нескольких программных операций карманного калькулятора. Здесь s — количество детей в сибстве, n, - число сибств размера s, r -число пораженных сибсов, р - тестируемое сегрегационное отношение, q = 1 — p. Чтобы вычислить ожидаемое значение S Es(r) для всего набора имеющихся сибств, нужно просуммировать соответствующие ожидаемые значения Es(r). Например, если семейные данные содержат 5 сибств размера 6 с двумя пораженными сибсами и одно сибство размера 8 с тремя пораженными сибсами, если каждое из этих сибств имеет одного пробанда (единичный отбор, k = 0) и если ожидаемое сегрегационное отношение равно 0,25 (рецессивное наследование), то ожидаемая численность пораженных для всего набора сибств получается следующим образом:
| 
| | Наблюдаемое число пораженных сибсов равно 5x2+1x3=13. Теперь эти два значения можно сравнить друг с другом, используя формулу χ = (О — E)/V, дисперсия вычисляется по формуле
| 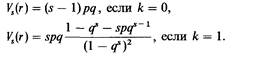
| | Дисперсия одного сибства составит
| 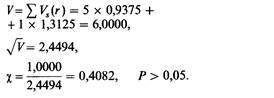
| | В табл. П. 3.1 представлен пример вычислений, связанных с генетическим анализом глухонемоты.
| | Оценка сегрегационного отношения в семейных данных. Описанный выше метод тестирования отвечает лишь на вопрос, согласуется ли имеющийся набор эмпирических численностей с их значениями, ожидаемыми на основе конкретной генетической гипотезы. Однако чаще такая гипотеза неочевидна. Следовательно, целесообразнее
|
| Таблица П.3.1. Тестирование сегрегационного отношения для глухонемоты в соответствии с априорным методом: предполагается, что брак между фенотипически непораженными генотипически представляет собой брак гетерозигот Аа х Аа
| 
| 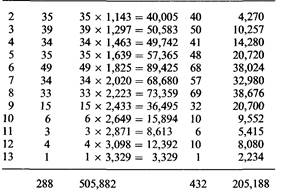
| | оценивать сегрегационное отношение. Первыми такими методами были вайнберговские "Geschwistermethode" (сибсовый метод) и "Probandenmethode" (пробандовый метод). Сибсовый метод применяется тогда, когда все пораженные сибсы являются одновременно и пробандами, т.е. когда k = 1. В этом случае для каждого пораженного сибса подсчитывают число его непораженных и пораженных сибсов. Например, сибство может содержать 6 членов, из которых трое поражены, а трое здоровы. Сибсовый метод дает следующий результат: пораженных будет 3x2 = 6 сибсов, а непораженных -3 х 3 = 9 сибсов (у каждого из трех пораженных имеем по два пораженных и три непораженных сибса). Оцениваемое сегрегационное отношение равно
| 
| | Если не все пораженные сибсы зарегистрированы в качестве пробандов, то упомянутая выше процедура преобразуется так, чтобы подсчет вести только для пробандов. Преобразованная процедура получила название пробандового метода. Если каждое
|
190 Приложение 3
| сибство было зарегистрировано через одного пробанда, то подсчет осуществляется только один раз. Для упомянутого выше сибства это означает p = 2/5 = 0,4 (случай k = 0). Для одного-единственного сибства две оценки для k = 1 и k = 0 идентичны. Однако они могут различаться, если выборка содержит много сибств разного размера. В этом случае оценка для k = 1 дает наибольшее значение р, а для k = 0 - наименьшее. Позже были разработаны более сложные методы оценки. Один из них предложил Финна [663]. Мы опишем его в версии Кэлина [729]. Для каждого сибства вычисляется взвешенный шанс
| 
| | здесь s— число всех сибсов, а r -число пораженных сибсов соответственно, и
| 
| | Взвешенные шансы Ws Ys и сами веса Ws суммируются по отдельности для всех сибсов. То значение р, для которого частное
| 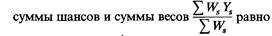
| | р, и есть оценка ρ истинного сегрегационного отношения. Кроме случаев единичного отбора (k = 0), значение р можно вычислить лишь итеративно. Начинают с первого приближения p1 оценки р, в качестве которого можно принять оценку, получаемую по пробандовому методу Вайнберга
| 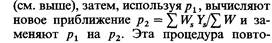
| ряется до тех пор, пока р2 не становится практически равным р1. Описанное вычисление можно упростить следующим образом. Если р2 больше pt (это означает, что p 1 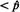 ), то вычисление повторяется с большими значениями р1, пока р2 не станет меньше, чем р1. Наоборот, если р2 исходно меньше, чем р1 (это означает, что ρ1 ), то вычисление повторяется с большими значениями р1, пока р2 не станет меньше, чем р1. Наоборот, если р2 исходно меньше, чем р1 (это означает, что ρ1 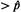 ), ),
|
| то ρ1 уменьшается до тех пор, пока р2 не станет больше, чем ρ1. Если в процессе вычисления р оказывается между р1 и р2, то оно вычисляется с помощью линейной интерполяции. Значение р можно представить как результат пересечения двух прямых линий
| 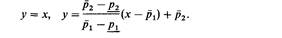
| | Правые части этих двух уравнений приравниваются, и полученное уравнение решается относительно х, что дает p). Дисперсию вычисляют следующим образом:
| 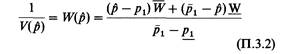
| | (линейная интерполяция между весами W и W, соответствующими ρ1 и р1). Эта процедура будет продемонстрирована ниже на практическом примере. Для k = 0 окончательная оценка р равна
| 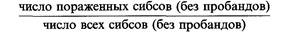
| | (пробандовый метод Вайнберга) и достигается уже на первом шаге итераций.
| | Давайте снова рассмотрим наш пример: сибство с s = 6 детьми, из которых r = 3 поражены. При полном отборе (k = 1) следующий шанс вычисляется, начиная с предварительной оценки р1 = 0,45,
| 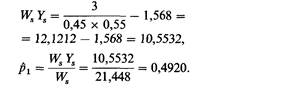
| | Здесь численные значения Bs и Ws вычисляются в соответствии с уравнениями П.3.1. Поскольку вычисленное значение р1 выше первоначального значения 0,45, то вычисление повторяется с р2 = 0,5:
| 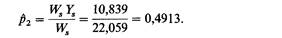
| | Истинное значение р находится между этими двумя оценками, оно может быть найдено с помощью интерполяции.
|
Дата добавления: 2015-12-16 | Просмотры: 684 | Нарушение авторских прав
|


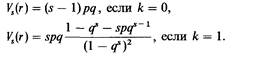
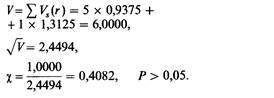





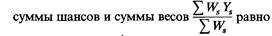
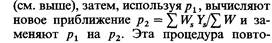
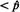 ), то вычисление повторяется с большими значениями р1, пока р2 не станет меньше, чем р1. Наоборот, если р2 исходно меньше, чем р1 (это означает, что ρ1
), то вычисление повторяется с большими значениями р1, пока р2 не станет меньше, чем р1. Наоборот, если р2 исходно меньше, чем р1 (это означает, что ρ1 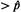 ),
),