АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Приложение 4 209

Рис. П.4.8. Отношение частот среди сибсов пробандов в браках пораженный х здоровый и здоровый х здоровый (R 2 = Q2,1/Q1,1) в диаллельной (штриховые линии) и мультифакториальной (сплошные линии) моделях [746].

основном на интуитивной основе, совместимы при анализе.

Важным параметром является наследуемость h². Ее следует оценить прежде всего. На практике это можно сделать двумя независимыми способами: используя уровни конкордантности МЗ близнецов или сравнивая частоту Q среди родственников пробандов с популяционной частотой Р. Первый метод дает H², а не h², но можно надеяться, что разность незначительна. Этот аспект обсуждается в разд. 3.8 и приложении 6. Второй метод зависит от свойств мультифакториальной модели, которые не всегда реалистичны и контролируемы.

Фолконер [654; 655] предложил принцип, который формально аналогичен проведению селекционного эксперимента в количественной генетике. Пусть G будет средней подверженностью в популяции, А — средней подверженностью пораженных, R -средней подверженностью родственников (данной степени родства) пораженных. Тогда отношение разностей R - G («ответ»)

и A - G («селекционный дифференциал») равно коэффициенту регрессии b подверженности родственников на подверженность пробандов

При указанных выше предположениях о подверженности (нормальное распределение со средней 0 и дисперсией 1) левая часть равна коэффициенту корреляции подверженностей

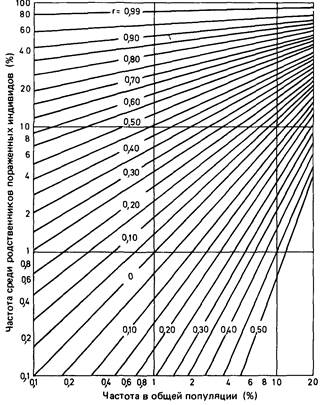
совпадающему с коэффициентом родства (например, b = ¹/₂ для родственников первой степени родства). Знаменатель правой части можно вычислить из (стандартного) нормального распределения, используя расстояние между популяционной средней и пороговым значением, соответствующим популяционной частоте P признака. Фолконер предложил получать значение числителя как разность между пороговым зна-

210 Приложение 4

Рис. П.4.9.. Таблица для получения оценки h2 из частоты (в %) признака в общей популяции и среди родственников пробандов первой степени родства. Например, если частота заболевания составляет 0,2% в общей популяции и 4% среди детей пробандов, то это соответствует коэффициенту корреляции r= 0,40, и поскольку h2 =	= 2 x r, то наследуемость h2 = 0,8. Обычно применяется формула h2 = r/R. Здесь R -мера родства, которую можно получить из формул для h2 в разд. 3.6.1.5. Например, R=1/2 для родственников первой степени родства, R = = 1/4 для родственников второй степени родства и R = 1 для МЗ близнецов [875а].

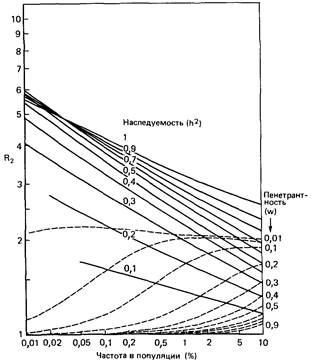
чением, соответствующим частоте Q признака среди родственников, и пороговым значением для популяции. Улучшенная номограмма (рис. П.4.9) с коэффициентом корреляции r подверженностей пробанда и родственника вместо h² была опубликована Смитом [880]. Эта номограмма охватывает также отрицательные значения h ² (ниже и справа от нулевой линии на рис. П.4.9). Отрицательные значения биологически бессмысленны, но, будучи следствием малого объема выборки, могут использоваться в случае объединения нескольких выборок для получения обобщенной оценки.

Сравнение значений, ожидаемых на основе этих моделей, с наборами реальных данных. Номограммы на рис. П.4.1-П.4.8 можно использовать для сравнения реальных семейных и близнецовых данных с ожидаемыми на основе двух моделей. Часто такое оценивание несет на себе интуитивный отпечаток того, какая модель рассматривается априори как более близкая к истине. Заметим, что сравнения неэффективны, если проводятся раздельно для родственников разных степеней родства: даже если каждое из них не позволяет отвергнуть какую-либо одну из двух моделей, то на основании общей картины частот среди родственников разной степени родства иногда все же можно отдать предпочтение одной из альтернатив. Кроме того, до сих пор молчаливо предполагалось, что популяционная часто-

Дата добавления: 2015-12-16 | Просмотры: 357 | Нарушение авторских прав