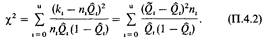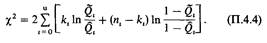АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Приложение 4 211

рамках конкретной модели. Теперь их нужно сравнить с действительно наблюдаемыми частотами. Точность, с которой модель описывает наблюдения, можно тестировать с помощью выражения

Когда справедлива нулевая гипотеза, т.е. когда распределение частот среди различных категорий родственников соответствует предполагаемому типу наследования, это выражение распределено приближенно как χ2 с u — 1 степенью свободы. Следовательно, если найденное значение выражения (П.4.2) больше табличного значения χ2, то нулевая гипотеза отвергается. Когда таким способом тестируются обе модели, то возможны четыре исхода:

1) нет различия между эмпирическими данными и какой-либо моделью: никакую модель нельзя исключить;

2) можно исключить только моногенную модель;

3) можно исключить только мультифакториальную модель;

4) исключаются обе модели.

Необходимо помнить, что даже альтернативы 2 и 3 не доказывают справедливость какой-либо одной из двух моделей. Одинаково хорошо эти данные можно объяснить многими другими моделями. На практике часто используется выражение

которое равно (за исключением дополнительной константы, не зависящей от параметров модели) натуральному логарифму выражения в уравнении П.4.1. Кроме уравнения П.4.2 для тестирования вполне пригодна формула

Мы не станем здесь описывать методы вычисления (они стандартны для математиков [746; 804]) МП-оценок параметров τ1 и τ2, т.е. тех значений параметров, для которых функция логарифма правдоподобия (уравнение ПАЗ) принимает максимальное значение.

Как мы поступаем на практике? Анализ широко распространенного заболевания - дело непростое и обычно требует помощи со стороны специалиста по статистической генетике. Иногда бывает трудно констатировать простые менделевские типы насле-

212 Приложение 4

дования из-за высокой частоты признака и сниженной пенетрантности. Однако даже искушенный специалист часто оказывается не в состоянии отличить моногенный признак с низкой пенетрантностью от мультифакториального признака.

Существенное значение имеет тщательный анализ гетерогенности. В этой группе широко распространенных признаков за диагнозом одной болезни часто могут скрываться несколько заболеваний с разными генетическими и негенетическими причинами. Кроме того, часто имеет место генотип-средовое взаимодействие, которое трудно оценить. Передачу признака в очень большой моногенной родословной можно легко разъяснить генетически, но результаты, полученные для этой группы родственников, могут оказаться неприменимыми к другим индивидам и их семьям. Прежде чем проводить генетический анализ, необходимо стандартизовать данные по возрасту начала, полу и другим факторам. Как правило, наиболее эффективным оказывается сравнение данных исследователя с различными генетическими моделями. Для большого числа моделей разработаны компьютерные программы. С их помощью можно определить соответствие реальных данных тому или иному типу наследования. Среди наиболее распространенных моделей-простое доминантное наследование, рецессивное наследование, полигенное наследование, полигенное наследование в комбинации с главным геном, негенетическая семейная агрегация. Однако даже при столь «исчерпывающей» обработке данных необходимо проявлять осторожность и не спешить с окончательными выводами.

Иногда незначительные изменения данных существенно их меняют. Вот почему надо с опаской относиться к принятию модели одного гена на основе такого анализа. С другой стороны, неудача при поиске моногенного наследования не обязательно означает, что нет главного гена. Важно, чтобы исследователь был осведомлен о биологическом, биохимическом и патофизиологическом фоне изучаемого заболевания. Применение новейших методов лабораторных исследований дает возможность выявить гетерогенность и приблизиться в познании конкретной патологии к генному уровню. Это намного более эффективно, чем использовать «фенотипические» диагнозы, которые на самом деле скрывают гетерогенность. Конечно, для многих болезней мы в настоящий момент можем удовольствоваться только этим. В общем случае наше проникновение в суть генетического механизма передачи таких болезней (например, шизофрении) будет полным, хотя на основе других факторов мы можем быть убеждены, что ключевую роль в их этиологии играют именно генетические факторы. Во всех случаях необходимы совместные усилия генетиков, статистиков и специалистов по изучаемой болезни.

Тестирование различных генетических моделей было проведено для ряда широко распространенных патологий, таких, как эпилепсия [611, 793], катехол-0-метилтрансферазная активность эритроцитов [666], гиперхолестеринемия [794], коронарная болезнь сердца [847] и гиперлипидемия [954]. Некоторые обобщения можно найти в [819-822].

Приложение 5

Диагностика зиготности

щем: какая доля всех близнецовых пар с одинаковой комбинацией генетических маркеров у самих близнецов и их родителей будет дизиготной? Или иначе: если предположить, что все близнецовые пары монозиготные, то как часто это предположение будет ошибочным? Общая формула Байеса имеет вид

где A1 и B-разные события, а А2 обозначает событие «не A1».

В нашем случае Р(А1/В) может быть вероятностью монозиготности среди всех близнецовых пар с идентичными группами крови. Тогда 1 — Ρ (A 1 /B)- вероятность близнецовой паре быть дизиготной или вероятность ошибки, когда близнецовая пара классифицирована как монозиготная. Р(А 1 - априорная вероятность МЗ близнецов среди всех близнецов в популяции. Это около 30% в европейских популяциях. Р(A 2) - априорная вероятность близнецовой паре быть дизиготной. Р(А2) = 1 — Р(А1) = 0,7. Уравнение П.5.1 можно упростить

Здесь Q - отношение ДЗ/МЗ в популяции (если 30% всех близнецовых пар это МЗ, то Q = 2,33). L - отношение условных вероятностей ДЗ и МЗ близнецов оказаться идентичными по данной комбинации генетических маркеров. Его значение можно вычислить путем перемножения Li для различных маркерных систем

214 Приложение 5

214 Приложение 5 Пример диагностики зиготности
	Отец	Мать	Оба близнеца
Пол
Группы крови	А2		A2
	MS/Ms	MS/Ms	MS/MS
	Kk	kk	Kk
	Fy (a + b+)	Fy (a - b +)	Fy (a - b +)
	R1r	R2r	rr
Сывороточные белки	Glm (-1)	Glm (-1, -2)	Glm(-l, -2)
	Km (-1)	Km(-l)	Km(-l)
	HP 2-2	HP 2-2	HP 2-2
	GC 2-2	GC2-1	GC 2-1
Изоферменты	ACP В	ACP AB	ACP AB
	PGM1 2 - 1	PGM1 2 - 1	PGM1 1 - 1
	AK1 1 - 1	AK1 1 - 1	AK1 1 - 1

Пример. В табл. П.5.1 и П.5.2 представлен пример. Просматривая список генетических маркеров, можно убедиться, что некоторые из них неинформативны: родители и дети оказываются генетически идентичными (IGHG(Gm), IGHG(Km), HP, AK). Для большинства других маркеров типы брака и, следовательно, ожидаемые сегрегационные отношения среди детей очевидны. Например, в системе GC отец гомозиготен 2-2, мать гетерозиготна 2-1, поэтому ожидаемое сегрегационное отношение среди детей составляет 1:1. Если близнец 1 имеет тип 2-1 и близнецы дизиготные, то вероятность для близнеца 2 быть 2-1 также составляет 0,50. Для групп крови АВО положение не столь очевидно, поскольку отец (с фенотипом А₂) может иметь генотипы А₂А₂ или А₂0. Если он А₂А₂, то оба близнеца должны иметь фенотип А₂, даже если они дизиготные. Если он А₂0, то вероятность, что второй близнец тоже А₂, равна 0,50. Иногда можно установить генотип родителя, например, если у другого ребенка группа крови 0. В остальном систему групп крови АВО можно считать неинформативной и не рассматривать. Два возможных генотипа следует ожидать в пропорции р₂: 2r, где р₂ и r -частоты аллелей А₂ и 0 в популяции. Тогда условная вероятность, что близнец имеет генотип А₂, может быть получена так

Однако это распределение генотипов является смещенным из-за исключения тех, кто однозначно идентифицирован на основании генотипа другого ребенка, имеющего группу крови 0. Для других систем крови вычисление производится следующим об-
Таблица П.5.2. Расчеты по данным таблицы П.5.1
Априорная вероятность	0,70	0,30
Условные вероятности 1}
Пол	0,50	1,00
АВО	0,50-1,00	1,00
MNSs	0,25	1,00
Kell (K)	0,50	1,00
Duffy	0,50	1,00
Rh	0,25	1,00
GC	0,50	1,00
ACP	0,50	1,00
PGM1	0,25	1,00
1)Условная вероятность того, что фенотип второго близнеца совпадает с фенотипом первого, если фенотип первого близнеца задан

Приложение 5 215

Приложение 5 215
Априорная вероятность	пол	MNSs	К	Fy	Rh	GС	АСР	PGM1
	х 0,5	х 0,25	х 0,5	х 0,5	х 0,25	х 0,5	х 0,5	х 0,25	= 0,0011,

Р(А₁/В) = 0,9989.

Следовательно, вероятность того, что близнецовая пара дизиготна, несмотря на ее конкордантность по всем информативным маркерным системам, крайне низка. Для всех практических целей предполагается монозиготность. Включение в анализ дополнительных менделевских маркеров повысит вероятность утверждения, что близнецовая пара монозиготна. Особенно эффективно для диагностики зиготности использование HLA-маркеров из-за огромной вариабельности этой системы. Заметим, что в нашем примере знаменатели в уравнении П.5.3 всегда были равны 1, т.е. МЗ близнецы всегда идентичны по всем своим маркерам. В принципе метод допускает также включение количественных признаков, по которым МЗ близнецы могут различаться, но в среднем более сходны, чемДЗ близнецы. В этом случае знаменатель в уравнении П.5.3 отличается от 1. Однако на практике такое расширение метода имеет небольшое значение.

Генотипы родителей могут быть неизвестны. В описанном выше примере генетические маркеры были известны не только в близнецовой паре, но и у родителей. Однако во многих случаях нет возможности обследовать родителей. При таких обстоятельствах для вычисления можно использовать известные генные частоты маркерных систем в популяции. Правила были сформулированы Смитом и Пенроузом (1955) [881]. Условная вероятность Р_{i ,ДЗ} того, что близнец 2 имеет тот же фенотип, что и близнец 1, если фенотип последнего i, вычисляется из частот типов брака в популяции (табл. П.5.3) и из относительного количества детей с разными генотипами, ожидаемого в этих браках (табл. П.5.4 и П.5.5). В табл. П.5.6-П.5.21 приведены

значения для Р_{i ,ДЗ} и обычно используемых полиморфных генетических систем. Эти генные частоты взяты главным образом из данных для популяций Северо-Восточной Европы.

Методы классической антропологии. Еще до того, как были открыты широко известные ныне системы генетического полиморфизма, для диагностики зиготности использовался довольно надежный метод, предложенный в 1924 г. Сименсом. Он основан на сравнении большого числа антропоскопических признаков; среди них цвет, форма и плотность волос, черты лица, детальная структура ряда лицевых областей (глаза, брови, цвет и структура радужной оболочки), детали области носа и рта, подбородок, уши, форма кистей и стоп, дерматоглифика, цвет и структура кожи (включая веснушки). Полезны также различные антропометрические характеристики тела, головы и лица. В антропологической литературе имеется список информативных признаков. На практике исследователь основывает свой диагноз не столько на сравнении отдельных черт, сколько на целостном об-

Таблица П.5.3. Таблица случайных браков для системы двух аллелей [881]
Брак	Частота	Дети

Таблица П.5.4. Частоты сибс — сибс для системы двух аллелей [882]
Генотип первого сибса	Генотип второго сибса
Фенотип первого сибса	Фенотип второго сибса
Таблица П.5.5. Относительные шансы в пользу дизиготности близнецовых пар в системе двух аллелей [882]
Генотип	Фенотип
Таблица П.5.6. Система АВО (3459 лиц из Англии [211])	Таблица П.5.7. Система MNSs (1419 лиц и; Англии [211])

Приложение 5 217

Таблица П.5.8. Система Резус (Rh): фенотипы обозначены по реакциям с антисыворотками + Ww, с, D, E, Cw, e (2000 лиц из Англии)	Таблица П.5.11. Система Даффи (Duffy) (1944 лиц из Англии)
	Таблица П.5.12. Система Кидд (Kidd) (4275 лиц со всего света)
Частоты аллелей
Таблица П.5.9. Система P (2345 лиц из Швеции)
Таблица П.5.13. Система Лютеран (Lutheran) (1373 лиц из Англии)
		Частоты аллелей

Таблица П.5.10. Система Келл (Kell) (l 108 лиц из Англии [211])

Приложение 5 218

Таблица П.5.14. Секреторы и несекреторы (1118 лиц из Ливерпуля)	Таблица П.5.18. Система IGKC (Km) (1234 лиц из ФРГ)
Таблица П.5.15. Система Нр	Таблица П.5.19. Система АК (108 лиц из ФРГ)
Частота аллелей
Таблица П.5.16. Система GC (678 лиц из ФРГ)	Таблица П.5.20. Система ACPI (528 лиц из ФРГ)
Частоты аллелей
Таблица Π 5 17 Система IGHG (Gm) (1234 лиц из ФРГ)	Таблица П.5.21. Система PGM1 (68 лиц из ФРГ)

Рис. П. 5.1. Трое МЗ близнецов (анфас и профиль) в возрасте 10 лет

Как мы поступаем на практике? Из предшествующего обсуждения может показаться, что исследование генетических маркерных систем является наиболее подходящим, а также достаточным методом для надежной диагностики зиготности. Однако этот вывод нуждается в некоторых пояснениях. Ошибка в определении только одной системы только у одного из двух близнецов приведет к ошибочной классификации МЗ пары как дизиготной, поэтому исследователь должен проверить вывод своими глазами. Если, несмотря на дискордантность, по маркерной системе при физиономическом сравнении близнецы кажутся монозиготными, необходимо настоять на повторном серологическом обследовании. Помимо возможности лабораторных ошибок изу-

Дата добавления: 2015-12-16 | Просмотры: 608 | Нарушение авторских прав

	Рис. П.5.2. и П.5.3. Физиономические детали трех МЗ близнецов с рис Π 5 1
Рис. П.5.4. МЗ близнецы в возрасте 10 лет Дискордантность по росту (по карликовости) низкорослый близнец, рожденный вторым, никогда не умел ходить и говорить У него обнаружено неспецифированное прогредиентное нарушение скелета Он умер вскоре после обследования У его брата-близнеца нормальный рост, но наблюдается билатеральное расщепление радужной оболочки глаз, которое отсутствует у близнеца-карлика [687]

При использовании материала ссылка на сайт medlec.org обязательна! (0.02 сек.)