|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология
|
Приложение 4 203
| cти широко распространенных заболеваний: мультифакториальная модель с порогом и модель простого доминантного типа наследования с неполной пенетрантностью. Мы будем следовать в основном анализу, проведенному Крюгером [746], поскольку этот автор четко изложил предположения и упрощения модели. О некоторых других, сходных подходах мы упомянем лишь кратко (детальное обсуждение было проведено в разд 3.6.2.2).
| | Пpocmoй диаллельный тип наследования с неполной пенетрантностью. Пусть пенетрантности генотипов АА и Аа будут w1 и w2 соответственно, а индивиды с генотипом aa всегда здоровы. Тогда частота признака в популяции равна
| 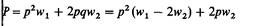
| | (p - частота аллеля А). Реалистическим упрощением этой модели для практических ситуаций будет предположение w 1 = 1 (полная пенетрантность гомозигот АА).
| | Мулътифакториальное наследование с пороговым эффектом. Обозначим через x фенотипическое значение подверженности заболеванию [654]. Это значение можно разбить на две компоненты, как показано в разд. 3.6.1. Предполагается, что средовое значение Ε не коррелирует с генотипическим значением G:
| 
| | и что генотипическое значение не содержит эпистатическую компоненту. G представляет собой сумму вкладов независимо действующих генов, и его распределение в популяции стремится к нормальному при увеличении их числа. Логично предположить, что G нормально распределено в популяции и что средовое отклонение Ε имеет нормальное распределение. При этих условиях фенотипическое значение x также будет распределено нормально.
| | Поскольку подверженность является гипотетической переменной, ее можно определить так, чтобы х, G и Ε имели среднюю 0, а фенотипическое значение x имело дисперсию 1. Тогда порог однозначно опреде-
|
ляется популяционной частотой Р, как та точка, которая делит стандартизованное нормальное распределение (нормальное распределение со средней 0 и дисперсией 1) на две части с частотами 1 — P и Р. Рассмотрим двух родственников определенной степени родства, выбранных из популяции случайным образом. Пара их подверженностей (x1, х2) является случайной величиной, которая имеет двумерное нормальное распределение. Когда задан коэффициент корреляции двух подверженностей 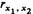 , это распределение полностью определено, и можно вычислить вероятность того, что какой-то один или оба родственника поражены. При описанных выше условиях коэффициенты фенотипической, генотипической и средовой корреляций подверженностей двух родственников связаны соотношением [488]: , это распределение полностью определено, и можно вычислить вероятность того, что какой-то один или оба родственника поражены. При описанных выше условиях коэффициенты фенотипической, генотипической и средовой корреляций подверженностей двух родственников связаны соотношением [488]:
| 
| | шинстве случаев корреляцию между средовыми компонентами Ε 1и Е 2двух родственников нельзя определить, поэтому предположим, что она равна 0. Кроме того, будет исследоваться только специальный случай Н2 = h2 (т. е. VG = VA) в соответствии с опытом количественной генетики, согласно которому неаддитивная компонента H 2 — h 2 обычно очень мала. Тогда справедливо следующее уравнение:
| 
| | ние, зависящее только от типа родства, а модель зависит только от параметров h 2 и Р. Дополнительное рассмотрение средовой компоненты E (что эквивалентно h 2 < 1) опровергает нереалистическое предположение о четком пороге. Он заменяется «пороговой областью», ширина которой задается с помощью VE. Предполагают, что внутри этой пороговой области вероятность проявления заболевания непрерывно увеличивается от 0 до 1.
| | Сравнение моногенной и мулыпифакториальной моделей. Ниже мы сравним эти модели для ряда значений популяционной ча-
|
Приложение 4

| | Рис. П.4.1. Поверхность двумерного нормального распределения подверженностей заболеванию двух индивидов Два порога обозначены штриховыми плоскостями Темные закрашенные области в переднем правом углу указывают вероятность Q того, что оба индивида поражены А Два неродственных индивида в панмиксной
| популяции Б Два родственника первой степени родства Интенсивно окрашенная область намного больше, чем на А, что указывает на возрастание риска для родственника быть пораженным, если пробанд страдает тем же заболеванием
|
стоты Р, для ряда значений пенетрантностей w в диаллельной модели и для различных предположений, касающихся h2, в мультифакториальной модели. Для диаллельной модели вычисление проводят непосредственно, когда предполагается, что регистрация проводилась в соответствии с единичным отбором (разд. 3.3). В случае мультифакториальной модели r = h 2/2 для родителей, сибсов и детей, r = h 2 для монозиготных близнецов. Исходя из этого и используя двумерное нормальное распределение подверженностей двух родственников I 1 и I 2, можно получить условную вероятность Q того, что I 2 поражен, если поражен
I 1, Q равно отношению вероятности того, что оба родственника поражены, к вероятности P 1, что поражен I 1. Q соответствует темно-серой области под поверхностью плотности нормального распределения на рис П.4.1, тогда как области, имеющие светло-серый цвет, соответствуют вероятностям событий. I 1 поражен, I 2нормальный и I 1 нормальный, I 2 поражен. На рис Π 4 1, А представлен случай двух неродственных индивидов. Риск каждого из них не зависит от риска другого: Q = Р. Это находит свое отражение в центральной симметрии поверхности плотности распределения На рис. П.4 1, Б показано совмест-
Приложение 4 205

| 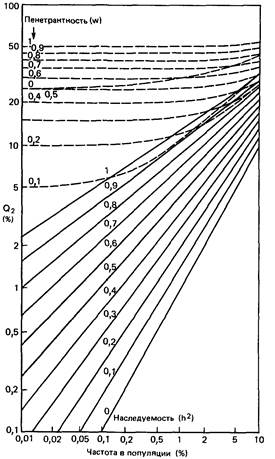
| | Рис. П.4.2. Частота признака среди детей (или родителей) пробандов (Q,) в диаллельной (штриховые линии) и мулътифакториальной (сплошные линии) моделях [746].
| Рис. П.4.3. Частота признака среди сибсов пробандов (Q2) в диаллельной (штриховые линии) и мультифакториальной (сплошные линии) моделях [746].
|
ное распределение подверженностей для родственников первой степени родства. В этом случае предполагается, что h 2 = 1 (и таким образом r = 1/2). Следствием этого является тот факт, что поражение I 1 увеличивает риск быть пораженным для родственника I 2: Q > Р. Объемы закрашенных участков под поверхностью плотности распределения можно вычислить с помощью численного интегрирования, на чем подробно мы останавливаться не будем (тетрахорические функции Пирсона, которые используются некоторыми авторами, обладают недостатками. Обсуждение этой проблемы см. в [746]).
На рис. П.4.2 и П.4.3 приведены результаты сравнения моделей. Используются следующие обозначения: Q1 - частота признака у детей или родителей пробандов, Q 2 - частота среди сибсов или дизиготных близнецов пробандов, Q 3 - частота среди монозиготных близнецов пробандов, Q 1,1 - частота среди сибсов пробандов с двумя здоровыми родителями, Q2,1 - частота среди сибсов пробандов, один из родителей которых поражен, Q 2,2 - частота среди сибсов пробандов, оба родителя которых поражены.
Диаграммы на рис. П.4.2 и П.4.3 очень просты. Они демонстрируют частоты в
Приложение 4
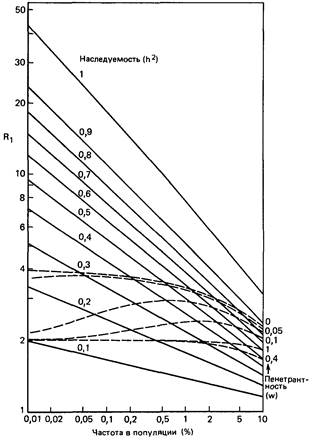
| Рис. П.4.4. Частота признака среди монозиготных и дизиготных близнецов пробандов (R1 = Q3/Q2) в диаллельной (штриховые линии) и мультифакториальной (сплошные линии) моделях [746].
|
двух моделях для детей (или родителей) и для сибсов безотносительно к типам брака родителей. Кривые обнаруживают определенное перекрывание для высокой частоты P (частота = 0,2-0,5% и выше) между доминантным наследованием с низкой пенетрантностью и мультифакториальным наследованием с высокой наследуемостью. С другой стороны, разделение двух моделей наследования признака с низкой частотой очень хорошее. Для монозиготных близнецов (на рисунке не показано) мультифакториальная модель всюду может имитировать поведение диаллельной модели. Однако противоположное, т.е. имитирование поведения мультифакториальной модели с помощью диаллельной, возможно только при высоких значениях h 2, но не при низких.
Дата добавления: 2015-12-16 | Просмотры: 587 | Нарушение авторских прав
|

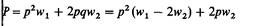

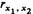 , это распределение полностью определено, и можно вычислить вероятность того, что какой-то один или оба родственника поражены. При описанных выше условиях коэффициенты фенотипической, генотипической и средовой корреляций подверженностей двух родственников связаны соотношением [488]:
, это распределение полностью определено, и можно вычислить вероятность того, что какой-то один или оба родственника поражены. При описанных выше условиях коэффициенты фенотипической, генотипической и средовой корреляций подверженностей двух родственников связаны соотношением [488]:





