 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Удельная электрическая проводимость растворов электролитов.Электрическая проводимость (электропроводность) обратна сопротивлению: L = Единицей измерения в системе СИ является обратный Ом (Ом–1) или сименс, См. Известно, что сопротивление любого проводника пропорционально его длине и обратно пропорционально сечению, S: R = ρ • где ρ – удельное сопротивление, Ом•м, характеризующее природу проводника. Подставляя уравнение (6.2) в уравнение в уравнение (6.1), получаем: L = где æ (каппа) – удельная электрическая проводимость, См/м, величина обратная удельному сопротивлению. Она характеризует свойства проводящей среды – раствора электролита. Удельная электрическая проводимость представляет собой проводимость 1м3 раствора помещенного между параллельными электродами площадью 1м2, находящимися на расстоянии 1м. В системе СИ единица измерения удельной электрической проводимости: См/м. В аналитической практике æ часто выражается в См/см. 1См/см = 102 См/м. Удельная электропроводность максимальна у растворов сильных кислот и оснований из-за их полной диссоциации и высокой подвижности ионов Н+ и ОН–. Наименьшей удельной электропроводностью обладают растворы слабых электролитов из-за низкой концентрации ионов. Удельная электропроводность зависит от концентрации электролита. С повышением концентрации она проходит через максимум, а затем уменьшается. Это связано, для сильных электролитов, с возрастанием мешающего межионного взаимодействия, а для слабых – со снижением степени диссоциации.
Молярная (эквивалентная) электрическая проводимость растворов электролитов. Молярная электрическая проводимость раствора электролита (λ, лямбда) равна удельной электрической проводимости его раствора с концентрацией 1 моль/м3. λ = где æ – удельная электропроводность, См/м, С – концентрация раствора электролита, моль/м3. В системе СИ λ выражается в См • м2/моль. λ = Поскольку в аналитической практике молярная концентрация выражается в моль/л (1моль/л = 103моль/м3), то для расчетов чаще используют формулу (6.6) λ = Влияние концентрации на молярную проводимость электролитов лучше проследить на графике зависимости λ от разбавления (1/С):

Рис.6.1. Зависимость молярной электрической проводимости от Разбавления.
С разбавлением растворов электролитов молярная электрическая проводимость увеличивается и стремится к максимальному значению, называемому предельной молярной электрической проводимостью (λ∞). Для слабых электролитов это объясняется тем, что при бесконечном разбавлении степень диссоциации достигает предельного значения, α =1. Отсюда можно рассчитать степень диссоциации слабого электролита при данной концентрации: α = и константу диссоциации: K = Для сильных электролитов при бесконечном разбавлении ионы удалены друг от друга на такие расстояния, что не мешают при их движении к электродам. Отсюда можно вычислить коэффициент электрической проводимости раствора: f = λ/λ∞ (6.9) Предельную молярную электропроводность иона λ∞К+ и λ∞An–можно вычислить и эти значения приведены в справочных таблицах С помощью закона Кольрауша можно рассчитать предельную молярную электрическую проводимость данного электролита. Предельная молярная электрическая проводимость электролита равна сумме предельных молярных проводимостей ионов, входящих в его состав. λ∞ = λ∞К+ + λ∞An– (6.10) Значение λ определяют экспериментально, λ∞ - рассчитывают по закону Кольрауша.
Дата добавления: 2015-12-16 | Просмотры: 1050 | Нарушение авторских прав |
 ;
;  = См (6.1)
= См (6.1) (6.2)
(6.2)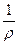 •
• 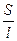 = æ •
= æ •  (6.3)
(6.3)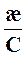 (6.4)
(6.4) , См∙м2/моль (6.5)
, См∙м2/моль (6.5)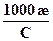 См∙см2/моль (6.6)
См∙см2/моль (6.6)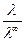 (6.7)
(6.7)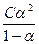 =
=  (6.8)
(6.8)