АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Линейное программирование

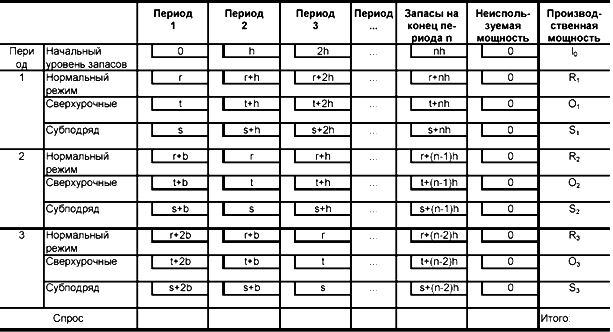
Модели линейного программирования являются методами получения оптимальных решений задач по распределению ограниченных ресурсов с точки зрения минимизации затрат либо максимизации прибыли. Основные ограничения моделей линейного программирования – необходимость линейной зависимости между переменными, невозможность постоянного регулирования объема выпуска и необходимость выбора единственной цели (например, минимизации затрат), вместо использования множественных целей (например, минимизация затрат при стабильном уровне рабочей силы).

Э.Х. Боуман1 предложил формулировать плановую проблему в виде модели, подобной транспортной модели программирования, как способ создания совокупных планов, балансирующих требования спроса с возможностями производства и минимизирующих затраты. Для использования этого подхода плановики должны оценить объем производства (предложение) при нормальном режиме работы, сверхурочных работах, субподрядах, а также уровень запасов на каждый период и соответствующие затраты на каждый показатель.

Структура транспортационной таблицы показана в табл. 6.2.

Систематический характер изменения затрат при продвижении по строке слева направо. Стоимость производства при нормальном режиме работы, сверхурочных работах, субподрядах является наименьшей в том случае, когда потребление (поставка, распределение и т.п.) продукции совпадает с периодом выпуска (пересечение столбца периода и строки регулярных производственных расходов). Если продукция может производиться в один период, но переносится на последующие периоды (движение по строке вправо), то добавляются затраты на хранение (h) за каждый период.

Хранение продукции в течение двух периодов добавляет к затратам единицу 2h, – независимо от того, была ли продукция выпущена при нормальном режиме работы, сверхурочно или по субподряду.

В случае переноса заказов на будущие периоды, затраты возрастают при движении по строке справа налево, начинаясь пересечении строки и столбца одного периода (например периода 3). Например, и некоторые товары были произведены в периоде 3 для выполнения задержанных заказов периода 2, то добавляются затраты на перенесение заказа (b). Если товары периода 3 предназначаются для выполнения заказов двух предыдущих периодов, то добавляются издержки 2b.

Таблица 6.2. Транспортационная таблица для совокупного планирования

Обозначения:

r — стоимость производства единицы продукции;

t — стоимость производства единицы при сверхурочных работах;

s — стоимость субподряда на единицу продукции;

h — затраты на хранение единицы в течение определенного периода;

b — стоимость задержки заказов на единицу в течение определенного периода;

n — число периодов в перспективе планирования.

Свободные мощности, как правило, добавляют к стоимости единицы продукции 0, хотя возможно ввести конкретные значения, если это необходимо. Начальным запасам добавляется стоимость 0, если они используются для удовлетворения спроса в периоде 1. Тем не менее, если запасы поддерживаются в последующих периодах, то добавляются затраты хранения (h) на каждый период. Если запасы поддерживаются на протяжении всего планового периода, то добавляется общая стоимость хранения h, умноженная на число периодов n.

Пример 4 иллюстрирует структуру и конечное решение транспортной модели для проблемы совокупного планирования. Если задержка заказов недопустима, показатели затрат в соответствующих ячейках должны быть настолько высоки, чтобы не допустить появления в решении невыполненных заказов.

Дата добавления: 2015-01-18 | Просмотры: 565 | Нарушение авторских прав