 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Приклади розв’язання задач. Задача 1. У 1905 році Бетсон вирішив перевірити справедливість законів Менделя і повторив досліди із схрещування гомозиготних рослин з жовтими й зеленими
Задача 1. У 1905 році Бетсон вирішив перевірити справедливість законів Менделя і повторив досліди із схрещування гомозиготних рослин з жовтими й зеленими насінинами. В F1 усі насінини були із жовтим забарвленням сім’ядолей, а в F2 при самозапиленні рослин, що виросли з гібридного насіння, одержано 3903 насінини із зеленими та 11902 з жовтими сім’ядолями. Чи підтвердив дослід Бетсона справедливість закону розщеплення? Довести це, використовуючи метод c2.
Кількість ступенів свободи (n) розраховується за формулою:
Якщо c2факт¹0 або коли c2 менше табличного значення, то різниці величин, що порівнюються, вважають випадковими (нульова гіпотеза). При значенні c2, рівному або більше того, що вказане в таблиці, нульова гіпотеза відкидається, тобто вважають різниці величин, які порівнюються, не випадковими, а закономірними. У нашому прикладі значення c2 = 0,77< c2табл.=3,841 (при р<0,05) та 6,635 (при р<0,01). Відповідь: дослід Бетсона підтвердив справедливість закону розщеплення Менделя (c2 = 0,77< 3,841). Задача 2. У матері нульова група крові, у батька група крови В. Чи можуть діти успадкувати групу крові матері? Які генотипи матері та батька? Роз’вязання: Р ♀ гр. О × ♂ гр. В Відомо, що генотип людей с групою крові О - i0 i0, отже, генотип матері - i0 i0. У людей с групою крові В генотип може бути або i0 IB, або IВ IВ. Діти можуть успадкувати групу крові матері тільки в тому випадку, якщо генотип батька IB i0.: Р ♀ i0 i0 × ♂ IB i0, Fа::1/2 IB i0: 1/2 i0 i0. Відповідь: діти можуть успадкувати групу крові матері тільки в тому випадку гетерозиготності батька за геном IB (генотип IB i0). Задача 3. Вроджений цукровий діабет обумовлений рецесивним аутосомним геном d з пенетрантністю у жінок - 90%, у чоловіків - 70%. Визначити ймовірність народження здорових та хворих дітей в родині, де обидва батьки є гетерозиготними носіями цього гена. Розв’язання: Р (F1): ♀ Dd × ♂ Dd, F2: ¼ DD: 2/4 D d: ¼ d d Отже, ймовірність появи нащадків dd у шлюбі Dd × Dd дорівнює 1/4 (25%). Але спостерігається неповна пенетрантність ознаки. У дівчинок вона дорівнює 90%. Події, що аналізуються, тобто імовірність народження дівчинки (1/2 = 50%) та імовірність успадкування діабету (25%), не пов’язані між собою і відбуваються незалежно. Тому загальна ймовірність появи дівчинки, хворої на діабет, дорівнюватиме: (0,25 × 0,9 × 0,5) × 100% = 11,25%. У хлопчиків пенетрантність дорівнює 70%. Імовірність народження хлопчиків (1/2 = 50%) та успадкування діабету також не пов’язані між собою і відбуваються незалежно.Отже, загальна ймовірність появи хлопчика, хворого на діабет, дорівнюватиме: (0,25 × 0,7 × 0,5) × 100% = 8,75%. Таким чином, імовірність народження дітей із цукровим діабетом у родині, де обидва батьки гетерозиготні, дорівнює: 11,25% + 8,75% = 20% (а не 25%). Решта дітей (с генотипами DD, Dd - 75% и dd - 5%), тобто із загальною імовірністю 80% мають бути здоровими. Відповідь: при гетерозиготності батьків імовірність народження здорових дітей у родині складає 80%, хворих – 20%. Задача 4. При схрещуванні між собою чорних мишей, завжди спостерігається чорне потомство. При схрещуванні між собою жовтих мишей 1/3 потомства опиняється чорною, а 2/3 – жовтою. Як це можна пояснити? Як можна перевірити правильність вашого припущення генетичними дослідами?
Відповідь: домінантний ген Ау у гомозиготному стані обумовлює жовте забарвлення шерсті і, крім того, летальний ефект, тобто є плейотропним. Перевірити правильність цього припущення можна за допомогою аналізуючого схрещування, схрещуючи жовтих і чорних мишей. В Fа буде завжди спостерігатися розшеплення у співвідношенні ½ жовті: ½ чорні: Р: ♀ Аyа х ♂аа Fа.: 1Ауа: 1 аа жовті чорні Отже, жовті миші завжди будуть гетерозиготними. Задача 5. За даними шведських генетиків, деякі форми шизофренії успадковуються як домінантні аутосомні ознаки. При цьому у гомозигот пенетрантність дорівнює 100%, у гетерозигот – 20%. Визначити ймовірність народження хворих дітей у сім’ї, де один із подружжя є гетерозиготним, і інший нормальний у відношенні ознаки, яка аналізується. Визначити ймовірність народження хворих дітей у шлюбі двох гетерозиготних батьків.
Для визначення ймовірності народження хворих дітей в сім’ї необхідно знайти добуток ймовірності носійства гена на ймовірність його проявлення. Отже, при гетерозиготності одного з батьків (хворого) знаходимо ймовірність появи в родині хворих дітей: 1/2 х 1/5 =1/10 або 10% У випадку гетерозиготності обох хворих батьків: Р'' ♀ Аа х♂ Аа F2:
Для гетерозигот пенетрантність 20% або 1/5. Хворі діти (гетерозиготи) можуть з’явитися з ймовірністю: 1/5 х 1/2 = 1/10 або 0,1. Тоді ймовірність народження хворої дитини в цьому шлюбі дорівнює сумі ймовірностей появи гомозигот і гетерозигот за даною ознакою: 0,25 + 0,1 = 0,35 або 35%. Відповідь: в першому випадку ймовірність народження хворої дитини 10%, в другому – 35%. Дата добавления: 2014-11-24 | Просмотры: 1533 | Нарушение авторских прав |
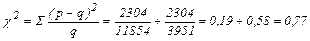 c2 =0,77
c2 =0,77