 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Статистичний аналіз модифікаційної мінливостіВивчення закономірностей модифікаційної мінливості проводять з використанням методів математичної статистики. При цьому необхідним є дотримання наступних умов: 1) матеріал, що піддається обробці, має бути генотипово однорідним (наприклад, рослини одного сорту, лінії, сім’ї); 2) вимірювання слід проводити з однаковою високою точністю; 3) спостереження мають бути багаторазовими, тому що тільки при масовості проявлення випадкові явища набувають закономірностей; 4) для аналізу використовуються не всі особини популяції (тобто генеральна сукупність), а тільки їхня частина – вибірка. Остання має бути репрезентативною, тобто відображати всю генеральну сукупність, та складатися зі значної кількості особин (від 30 – 100 і більше). Кожна особина генеральної сукупності потенційно повинна мати рівну можливість потрапити у вибірку, що досягається випадковим добором особин. При дотриманні цих умов використання статистичних методів є досить надійним і дозволяє виявити статистичні закономірності модифікаційної мінливості. Основними характеристиками фенотипної мінливості є варіаційний ряд та варіаційна крива. Варіаційний ряд – варіанти вибірки, розміщені в порядку збільшення або зменшення кількісної ознаки. Основними статистичними характеристиками варіаційного ряду є: середня арифметична ( Якщо окрему варіанту позначити х1, то при кількості варіант у варіаційному ряді (n) наведені показники складатимуть: ∑ х ∑ (х –
n n – 1 n
σ σ σ = √ σ2; V = ----------- х 100 %; m = ----------;
m m % = ----------- х 100
Варіаційна (модифікаційна) крива – графічне зображення ранжированого за даною ознакою варіаційного ряда. На вісі абсцис відкладається шкала кількісного вираження ознаки, на вісі ординат – частота особин. Характеризується середньою арифметичною даного ряда, величиною середнього квадратичного відхилення (σ). Чим більшою є σ при даній середній арифметичній, тим більше праворуч або ліворуч по абсциссі від неї заходять сторони варіаційної кривої. За умови відсутності генотипового різноманіття та суттєвих відхилень в умовах життя варіаційна крива наближається до кривої нормального розподілення (Гаусової кривої). Коефіцієнт успадкованості ознаки Н = Д: G; де Д – середнє значення ознаки у батьків; G – середнє значення цієї ж ознаки у нащадків. У генетиці людини (антропогенетиці) при проведенні близнюкових досліджень коефіцієнт успадкованості кількісної ознаки розраховується за формулою: Н = Vf - Vi: Vf., де V – фенотипові дисперсії відповідно ДЗ та МЗ близнюків (дизиготних та монозиготних близнюків). V = (х1 – х2)2: n, де х1 та х2 – значення ознак у ДЗ та МЗ близнюків; n – кількість пар близнюків. Коефіцієнт успадкованості з урахуванням особливостей дії генів розраховується за формулою: h2 = σА2 / σph2, σА2 = σg2 - σD2 - σI2, где h2 – коефіцієнт успадкованості, Часто σD2 та σD2 важко визначаються, тому σА2 =~ σg2. σg2 = σph2 - σE2, где σЕ2 – середовищна варіанса. Дата добавления: 2014-11-24 | Просмотры: 1015 | Нарушение авторских прав |
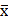 ) та її похибка (m), середнє квадратичне відхилення (σ), дисперсія або варіанса (σ2), коефіцієнт варіації (V), показник точності досліду (m %).
) та її похибка (m), середнє квадратичне відхилення (σ), дисперсія або варіанса (σ2), коефіцієнт варіації (V), показник точності досліду (m %).