 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Математические модели, описывающие зависимость доза - эффектВероятность обнаружения опухоли данного вида в обследуемой группе, не контактировавших с канцерогеном особей всегда выше нуля. Это связано с действием разнообразных факторов окружающей среды, провоцирующих опухолевый рост. Математическое моделирование призвано предсказать вероятность развития рака (р), как функцию дозы действующего токсиканта (d), с учетом этого обстоятельства. Наблюдаемыми и количественно оцениваемыми в ходе эксперимента эффектами могут быть смерть, потеря веса, число новообразований в группе. Непременными условиями моделирования являются: - достаточное количество изученных доз (минимум четыре) и животных, протестированных на каждой дозе; - учет "фоновых" значений оцениваемых параметров; - математическая форма представления зависимости "доза-эффект"; - адекватные методы оценки параметров модели. Возможны два способа учета "фона" при изучении зависимости "доза-эффект": 1. (Pd - P0)/(1 - P0) = F(d) 2. Pd = F(d + d0), где: Р0 - фоновая вероятность (частота) развития новообразования; Pd - вероятность развития новообразования при воздействии токсиканта в дозе d; F(d) - кумулятивное распределение позитивных ответов (канцерогенез) в зависимости от действующей дозы. В первом случае исходят из допущения, что ответ на воздействие определённой дозы не зависит от фоновой ответной реакции. Этот подход используют наиболее часто. Во втором случае принимается допущение, что вероятность развития эффекта есть следствие суммарного действия "фоновой" и действующей доз. Как правило, указанное различие в подходах к оценке не сказывается существенным образом на получаемых результатах, особенно при действии веществ в малых дозах. Для экстраполяции результатов, получаемых в опытах с действием больших доз, к условиям воздействия токсиканта в малых дозах, применяются математические модели разных видов. Наиболее часто используют логнормальную модель и модель логит-преобразования. Первая имеет вид: lg[ P/(1-P)] = a + b lgd, где а,b - параметры уравнения. Вторая математическая модель имеет вид: Y(P) = a + b lgd, где Y(P) - пробит, соответствующий частоте опухолей Р, a,b - параметры уравнения. Кроме указанных, используют и другие математические модели описания зависимости "доза-эффект" (таблица 5). Таблица 5. Математические модели, описывающие зависимость "доза-эффект", применяемые для оценки риска химического канцерогенеза
* d - доза токсиканта Дата добавления: 2015-02-06 | Просмотры: 1064 | Нарушение авторских прав |
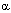 - b log d)b
- b log d)b
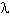 d
d