 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Вычисление двойных интеграловСамый простой способ вычисления двойного интеграла — сведение его к вычислению определенных интегралов. Этот способ можно реализовать, если область интегрирования является элементарной. Ниже перечисляются элементарные области интегрирования. 1.
2. Область
3. Область
Как вычислить двойной интеграл по области Замечание. Правые части формул (15.3) – (15.4) называются повторными интегралами. Интеграл, стоящий в скобках, называется внутренним. Другой интеграл называется внешним. Сначала вычисляют внутренний интеграл, а затем вычисляют внешний интеграл. Вместо выражений
пишут соответственно
Дата добавления: 2015-01-18 | Просмотры: 756 | Нарушение авторских прав |
 — прямоугольная область, расположенная между прямыми
— прямоугольная область, расположенная между прямыми  ,
,  ,
,  , а также между прямыми
, а также между прямыми  ,
,  ,
,  , и функция
, и функция  непрерывна в этой прямоугольной области
непрерывна в этой прямоугольной области 
 (15.3)
(15.3) ,
,  (
( ,
,  ). Если функция
). Если функция  (15.4)
(15.4) ,
,  (
( ,
,  ). Если функция
). Если функция  (15.5)
(15.5) ,
, 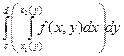
 ,
,  . ▲
. ▲