|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология
|
Доказательство. 1.Если , то из 3-го и 4-го свойства определенного интеграла вытекает
1. Если  , то из 3-го и 4-го свойства определенного интеграла вытекает , то из 3-го и 4-го свойства определенного интеграла вытекает
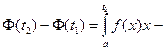     . .
2. Рассмотрим произвольную последовательность 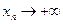 и докажем, что и докажем, что
 . Из свойства точной верхней грани следует, что найдется такое значение функции . Из свойства точной верхней грани следует, что найдется такое значение функции  , что , что  , где , где 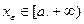 . Так как . Так как 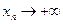 , то найдется такое число , то найдется такое число  , что , что  , если , если  . Теперь, из монотонности функции . Теперь, из монотонности функции  следует следует
 . .
Отсюда вытекает, что неравенство  справедливо, если справедливо, если  , т.е. , т.е. 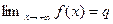 . ■ . ■
Дата добавления: 2015-01-18 | Просмотры: 640 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
|
