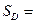|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Геометрическая интерпретация двойного интегралаПусть на области $$15.5 Криволинейный цилиндр с основанием Итак, объем Замечание. Если существует двойной интеграл Дата добавления: 2015-01-18 | Просмотры: 1269 | Нарушение авторских прав |
 задана непрерывная функция
задана непрерывная функция  , которая на этой области принимает неотрицательные значения.Криволинейным цилиндром называется тело
, которая на этой области принимает неотрицательные значения.Криволинейным цилиндром называется тело 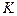 в пространстве, ограниченное сверху поверхностью
в пространстве, ограниченное сверху поверхностью  , снизу — областью
, снизу — областью 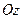 и проходящими через точки области
и проходящими через точки области  (рис 15.5) заменим прямым цилиндром с основанием
(рис 15.5) заменим прямым цилиндром с основанием 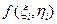 . Объем этого прямого цилиндра равен
. Объем этого прямого цилиндра равен 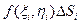 . Следовательно, интегральная сумма
. Следовательно, интегральная сумма  представляет собой сумму объемов прямых цилиндров, которая является приближенным значением объема тела
представляет собой сумму объемов прямых цилиндров, которая является приближенным значением объема тела  , то его естественно считать объемом тела
, то его естественно считать объемом тела 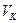 криволинейного цилиндра
криволинейного цилиндра 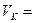
 .
. , то он равен объему прямого цилиндра с основанием
, то он равен объему прямого цилиндра с основанием 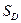 области
области