 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Решение. 15.12. Подынтегральная функция и функция больше нуля на промежутке15.12. Подынтегральная функция и функция
Так как интеграл 15.13. Подынтегральная функция и функция
Так как интеграл 15.14. Подынтегральная функция и функция
Так как интеграл 15.15. Подынтегральная функция и функция
Так как интеграл Задачи Исследовать сходимость следующих интегралов: 15.52. 15.55. Исследовать сходимость несобственных интегралов: 15.58. 15.61. Ответы 15.52. сходится. 15.53. расходится. 15.54. сходится. 15.55. сходится. 15.56. сходится. 15.57. сходится. 15.58. сходится. 15.59. сходится. 15.60. расходится. 15.61. сходится. 15.62. расходится. 15.63. сходится. ▲ Дата добавления: 2015-01-18 | Просмотры: 646 | Нарушение авторских прав |
 больше нуля на промежутке
больше нуля на промежутке 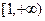 . Найдем предел частного этих функций, используя правило Лопиталя,
. Найдем предел частного этих функций, используя правило Лопиталя,
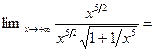
 .
. сходится, то интеграл
сходится, то интеграл  также сходится (теорема 15.2)
также сходится (теорема 15.2) больше нуля на промежутке
больше нуля на промежутке 
 .
.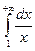 расходится, то интеграл
расходится, то интеграл  также сходится (теорема 15.2)
также сходится (теорема 15.2)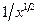 больше нуля на промежутке
больше нуля на промежутке 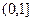 . Найдем предел частного этих функций, используя правило Лопиталя,
. Найдем предел частного этих функций, используя правило Лопиталя,
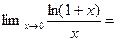
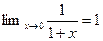 .
. сходится, то интеграл
сходится, то интеграл 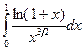 также сходится (теорема 15.3).
также сходится (теорема 15.3).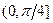 . Найдем предел частного этих функций, используя правило Лопиталя,
. Найдем предел частного этих функций, используя правило Лопиталя,

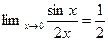 .
. расходится, то интеграл
расходится, то интеграл  также расходится (теорема 15.3). ●
также расходится (теорема 15.3). ●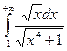 . 15.53.
. 15.53.  . 15.54.
. 15.54.  .
. . 15.56.
. 15.56. 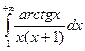 . 15.57.
. 15.57.  .
. . 15.59.
. 15.59.  . 15.60
. 15.60 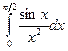 .
. . 15.62.
. 15.62. 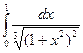 . 15.63.
. 15.63. 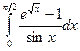 .
.