 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Доказательство. 1.Пусть сначала интеграл от функции сходится1. Пусть сначала интеграл от функции 2. Пусть интеграл 3. Пусть интеграл от функции Теорема 15.3. Пусть на промежутке Доказательство проводится аналогично. ■ Замечание. Использовать 2-й признак сходимости несобственных интегралов можно следующим образом. Надо положить Примеры. Исследовать на сходимость следующие интегралы: 15.12. 15.14. Дата добавления: 2015-01-18 | Просмотры: 637 | Нарушение авторских прав |
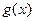 сходится. Так как существует предел
сходится. Так как существует предел  ,
,  , то из леммы следует ограниченность функции
, то из леммы следует ограниченность функции  на некотором промежутке
на некотором промежутке 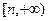 ,
,  , т.е.
, т.е.  или
или  , если
, если  . Из свойства 2 несобственных интегралов и условия теоремы следует, что интеграл
. Из свойства 2 несобственных интегралов и условия теоремы следует, что интеграл  сходится. Теперь из теоремы 15.1 вытекает сходимость интеграла
сходится. Теперь из теоремы 15.1 вытекает сходимость интеграла  , а из свойства 2 несобственных интегралов следует, что интеграл
, а из свойства 2 несобственных интегралов следует, что интеграл 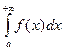 сходится.
сходится. . Теперь из 1 -го утверждения доказательства теоремы вытекает сходимость интеграла
. Теперь из 1 -го утверждения доказательства теоремы вытекает сходимость интеграла  .
. расходится. Докажем, что интеграл от функции
расходится. Докажем, что интеграл от функции 
 расходится методом от противного. Если предположить, что интеграл от функции
расходится методом от противного. Если предположить, что интеграл от функции  функция
функция 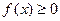 , а функция
, а функция  и существует предел
и существует предел  и
и  сходятся или расходятся одновременно.
сходятся или расходятся одновременно. и подобрать так значение
и подобрать так значение  , чтобы предел
, чтобы предел  . Затем определить при выбранном значении
. Затем определить при выбранном значении  . 15.13.
. 15.13.  .
.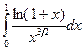 . 15.15.
. 15.15.  .
.