 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Интегрирование функции на ограниченном множествеДвойной интеграл от функции Пусть на множестве В каждой частичной области $$15.4 Определение 15.13. Сумма Значение числа Определение 15.14. Последовательность разбиений Определение 15.15. Число Так как определение предела интегральных сумм сформулировано в терминах пределов последовательности, то это позволяет перенести основные результаты теории пределов на этот новый вид предела. Определение 15.16. Число
Из этого определение следует, что
Замечание. Функция Дата добавления: 2015-01-18 | Просмотры: 764 | Нарушение авторских прав |
 , подобно определенному интегралу, определяется при помощи интегральных сумм функции
, подобно определенному интегралу, определяется при помощи интегральных сумм функции  определялись на отрезке
определялись на отрезке  . Естественным обобщением отрезка в пространстве
. Естественным обобщением отрезка в пространстве  является замкнутая и ограниченная область
является замкнутая и ограниченная область  .
. . Рассмотрим разбиение
. Рассмотрим разбиение  области
области  частичных областей
частичных областей  ,
, 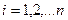 (рис.15.4). Диаметром
(рис.15.4). Диаметром  области
области  назовем наибольший среди диаметров частичных областей:
назовем наибольший среди диаметров частичных областей:  .
. , выберем точку
, выберем точку  .
. 
 называется интегральной суммой функции
называется интегральной суммой функции  зависит как от выбора разбиения
зависит как от выбора разбиения  .
.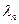 области
области  . Числовая последовательность
. Числовая последовательность  называется последовательностью интегральных сумм, если последовательность разбиений
называется последовательностью интегральных сумм, если последовательность разбиений  не накладывается никаких ограничений.
не накладывается никаких ограничений.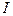 называется пределом интегральных сумм
называется пределом интегральных сумм  .
.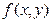 на области
на области  , функция
, функция 
 .
.