|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология
|
Простейшие свойства несобственных интегралов 2-го рода
Прочитайте:
- А. Свойства и виды рецепторов. Взаимодействие рецепторов с ферментами и ионными каналами
- Абразивные материалы и инструменты для препарирования зубов. Свойства, применение.
- Адгезивные системы. Классификация. Состав. Свойства. Методика работы. Современные взгляды на протравливание. Световая аппаратура для полимеризации, правила работы.
- Аденовирусы, морфология, культуральные, биологические свойства, серологическая классификация. Механизмы патогенеза, лабораторная диагностика аденовирусных инфекций.
- Альгинатные оттискные массы. Состав, свойства, показания к применению.
- Анатомия и гистология сердца. Круги кровообращения. Физиологические свойства сердечной мышцы. Фазовый анализ одиночного цикла сердечной деятельности
- Антигенные свойства
- Антитела (иммуноглобулины): структура, свойства. Классификация антител: классы, субклассы, изотипы, аллотипы, идиотипы. Закономерности биосинтеза.
- Антитела (строение, свойства, функции антител, феномены взаимодействия антител и антигенов).
- Атмосфера земли, ее структура и свойства. Природный физический и химический состав атмосферного воздуха. Физиолого-гигиеническое значение его составных компонентов.
|
|
Если функция  интегрируема на промежутке  при любом достаточно малом  и не ограничена в каждой окрестности точки  , то справедливы следующие утверждения.
1. Если  — первообразная функции на множестве  , то справедлива формула
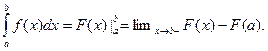
Доказательство. Применяя формулу Ньютона-Лейбница, имеем
 .
2. Интеграл  сходится тогда и только тогда, когда для любого числа  сходится интеграл  , причем справедлива формула
  .
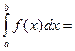3. Если интегралы и  сходятся, то интеграл  также сходится и справедлива формула
   .
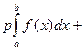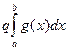Доказательства свойств 2 и 3 аналогичны доказательствам свойств 2 и 3 для несобственных интегралов 1-го рода. ■
Аналогичные свойства справедливы и для других несобственных интегралов 2-го рода.
Задачи
Вычислить интегралы
15.15.  . 15.16.  . 15.17.  . 15.18.  . 15.19.  .
15.20.  . 15.21.  . 15.22.  . 15.23.  .
15.24.  . 15.25.  . 15.26.  . 15.27.  .
15.28.  . 15.29.  . 15.30.  . 15.31.  .
15.32.  . 15.33.  .
Ответы
15.15.  , если  ; расходится, если  . 15.16. 1. 15.17.  . 15.18. расходится. 15.19.  . 15.20. 8. 15.21. расходится. 15.22. 6. 15.23.. 2 15.24.  . 15.25. расходится. 15.26.  . 15.27. расходится. 15.28.  . 15.29.  . 15.30.  , если  ; расходится, если  . 15.31.  . 15.32. расходится. 15.33.  .
Дата добавления: 2015-01-18 | Просмотры: 704 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
|
