Решение. Пустьфункция определена на промежутке и интегрируема на любом конечном отрезке
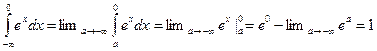 . ● . ●
Пустьфункция  определена на промежутке определена на промежутке 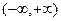 и интегрируема на любом конечном отрезке. и интегрируема на любом конечном отрезке.
Определение 15.3. Суммапределов 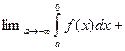 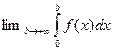 называется несобственным интегралом с бесконечным нижним и верхним пределом. Его обозначаютсимволом называется несобственным интегралом с бесконечным нижним и верхним пределом. Его обозначаютсимволом  и, следовательно, и, следовательно,
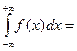 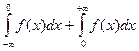 . .
Интеграл  сходится, если интегралы сходится, если интегралы 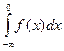 и и 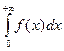 сходятся. Если же, хотя бы один из этих интегралов расходится, то расходится и интеграл сходятся. Если же, хотя бы один из этих интегралов расходится, то расходится и интеграл  . .
Дата добавления: 2015-01-18 | Просмотры: 667 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
|
