|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология
|
Второй признак сходимости
В некоторых случаях бывает затруднительно подобрать так функцию  или или 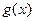 , чтобы на требуемом промежутке было справедливо неравенство , чтобы на требуемом промежутке было справедливо неравенство 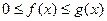 . Кроме того, необходимо, чтобы несобственный интеграл от функции . Кроме того, необходимо, чтобы несобственный интеграл от функции 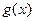 сходился или несобственный интеграл от функции сходился или несобственный интеграл от функции  расходился. В этих случаях полезен второй признак сходимости несобственных интегралов. Сначала докажем лемму, необходимую далее. расходился. В этих случаях полезен второй признак сходимости несобственных интегралов. Сначала докажем лемму, необходимую далее.
Лемма. Если существует предел 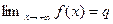 , ,  , то функция ограничена на некотором промежутке , то функция ограничена на некотором промежутке 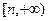 , , 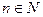 . .
Доказательство проведем методом от противного. Тогда в каждом промежутке 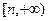 найдется такая точка найдется такая точка 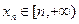 , в которой , в которой 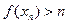 . Так как последовательность . Так как последовательность  — бесконечно большая и — бесконечно большая и  , то, , то, 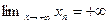 . Отсюда и из определения предела функции следует, что . Отсюда и из определения предела функции следует, что 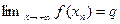 . Следовательно, последовательность . Следовательно, последовательность  ограничена, что противоречит условию ограничена, что противоречит условию 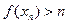 , , 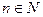 . ■ . ■
Теорема 15.2. Пусть на промежутке 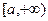 функция функция 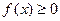 , а функция , а функция  и существует предел и существует предел  . Тогда интегралы . Тогда интегралы 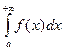 и и  сходятся или расходятся одновременно. сходятся или расходятся одновременно.
Дата добавления: 2015-01-18 | Просмотры: 720 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
|
