Несобственные интегралы второго рода
Определение 15.5. Пусть функция  интегрируема на промежутке интегрируема на промежутке  при любом достаточно малом при любом достаточно малом  и не ограничена в каждой окрестности точки и не ограничена в каждой окрестности точки  (рис. 15.2). (рис. 15.2).
$$ 15.2 $$ 15.3
Несобственным интегралом от этой функции на отрезке  называется предел называется предел
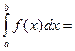  (15.1) (15.1)
Если предел в правой части равенства (15.1) существует (не существует), то несобственный интеграл называется сходящимся (расходящимся).
Дата добавления: 2015-01-18 | Просмотры: 767 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
|
