 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Решение. 15.10. Так как на промежутке неравенство справедливо, и интеграл расходится, то из теоремы 15.1 следует15.10. Так как на промежутке 15.11. Подынтегральная функция неограничена в окрестности верхнего предела интегрирования. На промежутке Задачи Исследовать сходимость интегралов: 15.34. 15.38. 15.42. Исследовать на сходимость несобственные интегралы: 15.46. 15.50. Ответы 15.34. сходится. 15.35. сходится. 15.36. расходится. 15.37. расходится. 15.38. сходится. 15.39. расходится. 15.40. сходится. 15.41. сходится. 15.42. сходится. 15.43. расходится. 15.44. сходится. 15.45. сходится. 15.46. сходится. 15.47. сходится. 15.48. расходится. 15.49. сходится. 15.50. сходится. 15.51. расходится. ▲ Дата добавления: 2015-01-18 | Просмотры: 644 | Нарушение авторских прав |
 неравенство
неравенство 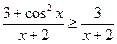 справедливо, и интеграл
справедливо, и интеграл  расходится, то из теоремы 15.1 следует, что интеграл
расходится, то из теоремы 15.1 следует, что интеграл 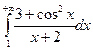 расходится.
расходится.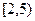 неравенство
неравенство 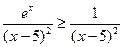 справедливо. Так как интеграл
справедливо. Так как интеграл 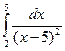 расходится, то из замечания к теореме 15.1 следует, что интеграл
расходится, то из замечания к теореме 15.1 следует, что интеграл 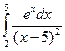 расходится. ●
расходится. ● . 15.35.
. 15.35. 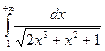 . 15.36.
. 15.36.  . 15.37.
. 15.37. 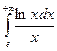 .
.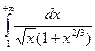 . 15.39.
. 15.39.  15.40.
15.40. 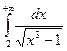 . 15.41.
. 15.41. 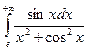 .
. . 15.43.
. 15.43. 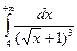 .15.44.
.15.44. 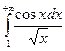 . 15.45.
. 15.45. 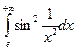 .
.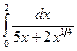 . 15.47.
. 15.47. 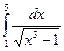 . 15.48.
. 15.48. 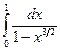 . 15.49.
. 15.49.  .
.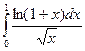 . 15.51.
. 15.51.  .
. 