 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Сравнение двух выборок. Основным параметрическим критерием для сравнения двух выборок является -критерий Стьюдента для независимых выборок (t-test for Independent Samples)Основным параметрическим критерием для сравнения двух выборок является Для вычисления статистики критерия существует ряд различных формул, учитывающих особенности ситуации его применения и, в частности, характер предположений о дисперсиях генеральных совокупностей, из которых извлечены выборки [1. С.169-172; 4. C.395-399; 14. С.83-85; 22. С.204-206]: · дисперсии известны и равны между собой; · дисперсии известны, но неравны между собой; · дисперсии неизвестны, но предполагается их равенство; · дисперсии неизвестны, их равенство не предполагается. Кроме того, существуют варианты критерия для случаев равных и неравных выборок (см., напр., [1. C.170], а также для связных и несвязных выборок (вариант для связных выборок будет рассмотрен в теме 8.1). Для психологических исследований наиболее обычной является ситуация, когда дисперсии генеральных совокупностей неизвестны, но предполагается их равенство между собой; при этом исследуемые выборки могут иметь различные объемы. В этом случае статистика критерия Стьюдента вычисляется по формуле [4. С.395; 7. C.72; 22. С.205]:
где
где
Критерий Стьюдента обсуждается во многих работах: · его непосредственное применение в психологических исследованиях рассмотрено в [1. C.169-174; 5; 13; 29]; · разнообразные примеры использования критерия приведены в [6-8; 15; 17; 18; 20]; · использование критерия в статистическом пакете SPSS обсуждается в [2; 35], в пакете Statistica for Windows – в [9-11], а в пакете Stadia – в [19]; · математико-статистические основания критерия рассмотрены в [4; 14; 16; 21-25; 28; 30; 31; 33]. Другим популярным параметрическим критерием является Из непараметрических критериев для сравнения двух выборок наиболее популярен Критерий Манна-Уитни является непараметрическим аналогом
где Критерий Манна-Уитни рассматриваются в многочисленных литературных источниках: · методика его применения в психологических исследованиях обсуждается в [1. C.101-110; 3. С.49-55]; · разнообразные примеры применения критерия приведены в [8; 15; 17; 27]; · использование критерия в статистическом пакете SPSS обсуждается в [2; 35], в пакете Statistica for Windows – в [9-11], а в пакете Stadia – в [19]; · математико-статистические основания критерия рассмотрены в [4; 14; 16; 21-25; 28; 31-33]. Далее рассмативаются решения задач, встречающихся при анализе психологических данных, в которых применяются критерии выявления различий в уровне признака для двух выборок. Задача 7.1-1. Применение критерия Манна-Уитни для выявления Условие: с помощью методики «Личностный дифференциал» обследованы студенты психологического факультета (выборка A) и других факультетов (выборка B). Результаты, полученные по фактору «Сила Я», приведены в табл. 7.1-1. Найти: можно ли утверждать, что выборки отличаются друг от друга по показателю фактора «Сила Я»? Таблица 7.1-1 Дата добавления: 2015-01-18 | Просмотры: 2046 | Нарушение авторских прав |
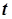 - критерий Стьюдента для независимых выборок (t-test for Independent Samples). Вариант критерия, предназначенный для сравнения средних величин выборок, ориентирован на проверку гипотезы однородности, т.е. гипотезы о том, что обе выборки извлечены из одной и той же генеральной совокупности. Обычно при применении критерия Стьюдента предполагается, что обе выборки извлечены из генеральных совокупностей, имеющих нормальные распределения. Однако специальные исследования показали, что этот критерий, особенно при больших объемах выборок, является устойчивым к отклонениям исследуемых генеральных совокупностей от нормальных, следовательно, вообще говоря, он может применяться и к выборкам из негауссовских генеральных совокупностей, но при этом истинные значения уровня значимости и мощности критерия будут незначительно отличаться от заданных [4. C.395] и, строго говоря, должны оцениваться с помощью специальных приемов. Поэтому в «чистом виде» критерий Стьюдента все же требует нормальности распределений выборок.
- критерий Стьюдента для независимых выборок (t-test for Independent Samples). Вариант критерия, предназначенный для сравнения средних величин выборок, ориентирован на проверку гипотезы однородности, т.е. гипотезы о том, что обе выборки извлечены из одной и той же генеральной совокупности. Обычно при применении критерия Стьюдента предполагается, что обе выборки извлечены из генеральных совокупностей, имеющих нормальные распределения. Однако специальные исследования показали, что этот критерий, особенно при больших объемах выборок, является устойчивым к отклонениям исследуемых генеральных совокупностей от нормальных, следовательно, вообще говоря, он может применяться и к выборкам из негауссовских генеральных совокупностей, но при этом истинные значения уровня значимости и мощности критерия будут незначительно отличаться от заданных [4. C.395] и, строго говоря, должны оцениваться с помощью специальных приемов. Поэтому в «чистом виде» критерий Стьюдента все же требует нормальности распределений выборок. , (7.1-1)
, (7.1-1) - средние значения для первой и второй выборки
- средние значения для первой и второй выборки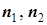 - объемы выборок;
- объемы выборок; - объединенная оценка выборочной дисперсии
- объединенная оценка выборочной дисперсии , (7.1-2)
, (7.1-2) и
и  - оценки дисперсий для соответствующих выборок, вычисляемые, в свою очередь, по формулам:
- оценки дисперсий для соответствующих выборок, вычисляемые, в свою очередь, по формулам: (7.1-3)
(7.1-3)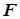 - критерий Фишера (
- критерий Фишера ( - критерий Манна-Уитни (Mann-Whitney U test), так как он имеет весьма слабые ограничения на объемы выборок (в каждой выборке должно быть не менее трех измерений), а кроме этого позволяет сравнивать между собой выборки разного объема [3. C.50]. Критерий предназначен, в частности, для проверки нулевой гипотезы о том, что средние значения двух выборок не отличаются друг от друга. Иногда эту гипотезу формулируют так: предполагается, что обе независимые выборки взяты из одной и той же генеральной совокупности.
- критерий Манна-Уитни (Mann-Whitney U test), так как он имеет весьма слабые ограничения на объемы выборок (в каждой выборке должно быть не менее трех измерений), а кроме этого позволяет сравнивать между собой выборки разного объема [3. C.50]. Критерий предназначен, в частности, для проверки нулевой гипотезы о том, что средние значения двух выборок не отличаются друг от друга. Иногда эту гипотезу формулируют так: предполагается, что обе независимые выборки взяты из одной и той же генеральной совокупности.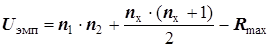 , (7.1-4)
, (7.1-4) , (7.1-5)
, (7.1-5) ,
, 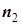 - объемы, соответственно, первой и второй выборки;
- объемы, соответственно, первой и второй выборки; и
и  - суммы рангов, соответственно, по первой и по
- суммы рангов, соответственно, по первой и по - наибольшая из двух ранговых сумм;
- наибольшая из двух ранговых сумм;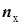 - объем выборки, имеющей наибольшую сумму рангов.
- объем выборки, имеющей наибольшую сумму рангов.