 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Сравнение двух выборокИз параметрических критериев выявления достоверности сдвига для двух выборок наиболее часто используют вариант Среди непараметрических критериев достоверности сдвига для двух выборок наиболее популярным является В случае применения одностороннего критерия Вилкоксона гипотеза Порядок применения критерия Вилкоксона следующий: · определяются «сдвиги» (разности между парными значениями первой и второй выборок), а также их типичное (преобладающее) направление; · абсолютные величины сдвигов ранжируются; · вычисляется эмпирическое значение статистики критерия, представляющее собой сумму рангов, соответствующую сдвигам в нетипичном (более редком) направлении; · полученное эмпирическое значение статистики критерия сравнивается с критическими значениями (табличными), соответствующими определенным уровням значимости (обычно 0,01 и 0,05); · в зависимости от результата принимается решение о принятии или отклонении нулевой гипотезы. Таким образом, эмпирическое значение статистики критерия рассчитывается по следующей формуле [1. C.81; 3. C.92]:
где
Обсуждение критерия Вилкоксона имеется в работах [1. С.78-82; 3. С.87-94; 4; 6-8; 11; 14-16]; технология его применения в статистических пакетах обсуждается в следующих работах: для пакета SPSS - [2. С.103-104; 18], для пакета Statistica for Windows – [5. С.517], для пакета Stadia – [10]. Задача 8.1-1. Применение критерия Вилкоксона для выявления Условие: в кризисном центре «Гортензия» был проведен тренинг на снижение уровня тревожности у женщин, подвергшихся домашнему насилию. Было сделано два замера уровня тревожности: до проведения тренинга (выборка A) и после (выборка B). Результаты приведены в табл. 8.1-1. Найти: можно ли утверждать, что после тренинга наблюдается достоверный сдвиг в сторону снижения уровня тревожности? Таблица 8.1-1 Показатели личностной тревожности
Решение: 1. Типичным направлением сдвига после прохождения тренинга в показателях личностной тревожности является уменьшение их значений. Соответственно нетипичным направлением сдвига является увеличение показателей тревожности. 2. Выдвигаем гипотезы · · 3. Применим для решения задачи пакет SPSS. Запускаем пакет и вводим исходные данные: для выборки A – в первый столбец таблицы (var00001), для выборки B – во второй (var00002). 4. В главном меню последовательно выбираем команды: Statistics (Статистики) – Nonparametric tests (Непараметрические критерии) – 2 Related samples (2 связанные выборки). 5. В окне критериев для связанных выборок задаем сравниваемые переменные (var00001 и var00002) и в поле Test type (Тип теста) флажком устанавливаем тип используемого критерия – Wilcoxon (Критерий Вилкоксона). 6. Нажав ОК, выполняем саму проверку и переходим в окно SPSS Viewer (Просмотр результатов). В таблице Test statistics (Результаты теста) находим значение статистики критерия Ответ: под влиянием проведенного тренинга существует статистически достоверный сдвиг показателей тревожности в сторону уменьшения. Задача 8.1-2. Применение критерия Стьюдента для выявления Условие: при приеме на работу сотрудников страховой компании было проведено исследование уровня профессиональной пригодности на выборке из 90 человек (выборка A, данные уже использовались в задаче 6.1-1, табл. 6.1-1). Затем с сотрудниками был проведен цикл специальных занятий и тренингов по развитию профессионально важных качеств, после окончания которых повторно замерялся уровень профессиональной пригодности (выборка B). Полученные данные приведены в табл. 8.1-2. Найти: можно ли утверждать, что после обучения наблюдается достоверный сдвиг в показателях профпригодности? Таблица 8.1-2 Уровень профессиональной пригодности до и после
Продолжение табл. 8.1-2
Решение: 1. Выдвигаем гипотезы: 2. Применим для решения пакет SPSS. Сначала, используя алгоритм действий задачи 8.1-1, определим достоверность сдвига по критерию Вилкоксона. Получаются следующие результаты: значение статистики критерия Вилкоксона равно -1,864, двухсторонняя асимптотическая значимость равна 0,062, т.е., согласно критерию Вилкоксона, сдвиг статистически недостоверен (не удовлетворяет уровню значимости 0,05), следовательно, альтернативная гипотеза должна быть отвергнута. 3. Как отмечалось в теоретическом разделе, в случаях, когда эмпирические данные распределены по нормальному закону, параметрические критерии являются более мощными по сравнению с непараметрическими. Эти соображения наводят на мысль использовать для оценки достоверности сдвига более мощный по сравнению с критерием Вилкоксона параметрический критерий Стьюдента. Но для его корректного применения необходимо предварительно проверить соответствие распределения данных нормальному закону. Алгоритм такой проверки в пакете SPSS рассмотрен при решении задачи 7.1-2. Выполнив шаги 2-5 из решения этой задачи, в окне SPSS Viewer (Просмотр результатов) находим таблицу Tests of Normality (Критерии нормальности), содержащую значения для теста Колмогорова-Смирнова: Statistic (Статистика) равна 0,076 для первой выборки и 0,078 - для второй при одинаковом уровне значимости 0,200. Полученные результаты свидетельствуют о том, что распределения и первой, и второй выборки не отличаются от нормального закона. Следовательно, мы можем применить для оценки достоверности сдвига критерий Стьюдента для парных выборок. 4. Для применения этого варианта критерия Стьюдента данные должны быть занесены в отдельные столбцы, а не в один при использовании группирующей переменной. Изменяем это, используя средства редактирования данных пакета SPSS. В результате данные по двум выборкам оказываются занесены в столбцы, соответствующие переменным var00001 и var00002. 5. В главном меню программы последовательно выбираем команды: Statistics (Статистики) – Compare means (Сравнение средних) – Paired-Samples T Test ( 6. В открывшемся окне 7. Нажав на кнопку ОК, выполняем саму проверку и переходим в окно SPSS Viewer (Просмотр результатов). В таблице Paired Samples Test (Тест для парных выборок) находим значение статистики критерия Стьюдента Ответ: существует статистически достоверный сдвиг показателей профпригодности под влиянием проведенного обучения. Дата добавления: 2015-01-18 | Просмотры: 2127 | Нарушение авторских прав |
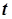 - критерия Стьюдента, предназначенный для связанных выборок. Его особенности рассмотрены в [1. C.172-174; 6. С.85-87; 9; 15]; технология его применения в пакете SPSS обсуждается в [2. С.82-87; 18], в Statistica for Windows – в [5. С.482-483], в Stadia – в [10].
- критерия Стьюдента, предназначенный для связанных выборок. Его особенности рассмотрены в [1. C.172-174; 6. С.85-87; 9; 15]; технология его применения в пакете SPSS обсуждается в [2. С.82-87; 18], в Statistica for Windows – в [5. С.482-483], в Stadia – в [10]. - критерий Вилкоксона (Wilcoxon signed-rank test - знаковый ранговый критерий Вилкоксона, критерий знаковых рангов Уилкоксона, критерий Вилкоксона для сопряженных пар). Он применяется для сравнения выборок с попарно сопряженными вариантами.
- критерий Вилкоксона (Wilcoxon signed-rank test - знаковый ранговый критерий Вилкоксона, критерий знаковых рангов Уилкоксона, критерий Вилкоксона для сопряженных пар). Он применяется для сравнения выборок с попарно сопряженными вариантами.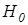 утверждает, что интенсивность сдвигов в типичном направлении не превосходит интенсивности сдвигов в нетипичном направлении; соответственно гипотеза
утверждает, что интенсивность сдвигов в типичном направлении не превосходит интенсивности сдвигов в нетипичном направлении; соответственно гипотеза 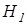 утверждает обратное [3. С.88]. Для двухстороннего критерия Вилкокс она нулевая гипотеза состоит в отсутствии эффекта направленного воздействия, альтернативная – в присутствии такого эффекта.
утверждает обратное [3. С.88]. Для двухстороннего критерия Вилкокс она нулевая гипотеза состоит в отсутствии эффекта направленного воздействия, альтернативная – в присутствии такого эффекта.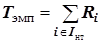 , (8.1-1)
, (8.1-1)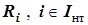 - ранги нетипичных (более редких) сдвигов,
- ранги нетипичных (более редких) сдвигов,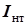 - множество индексов (номеров) таких сдвигов.
- множество индексов (номеров) таких сдвигов. = -3,300, Asymp. Sig. (2-tailed) (Асимптотическая двухсторонняя значимость) равна 0,001 (заметим, что в пакете SPSS реализован двухсторонний вариант критерия). Полученные результаты свидетельствуют о наличии статистически достоверного сдвига в распределении показателей тревожности до и после проведения тренинга, следовательно, гипотеза
= -3,300, Asymp. Sig. (2-tailed) (Асимптотическая двухсторонняя значимость) равна 0,001 (заметим, что в пакете SPSS реализован двухсторонний вариант критерия). Полученные результаты свидетельствуют о наличии статистически достоверного сдвига в распределении показателей тревожности до и после проведения тренинга, следовательно, гипотеза  -критерий для парных выборок).
-критерий для парных выборок).