 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Однофакторный дисперсионный анализЧасто применяемым методом проверки выборок на однородность является однофакторный дисперсионный анализ (ОДА, дисперсионный анализ по одному признаку), который в англоязычной литературе называется ANOVA (от слов «Analysis of Variance»; в отечественной литературе это выражение принято переводить как «Дисперсионный анализ»), либо One-way analysis of variance (Однофакторный дисперсионный анализ). Центральная идея ОДА заключается в следующем: исследователя интересует, существенно ли влияние на измеряемые переменные некоторого фактора, под которым понимаются либо эффекты каких-либо воздействий (обучения, тренингов, психокоррекционных курсов и др.), либо различные условия проведения измерений (временные, ситуационные, психологические и др.). Для выявления этого влияния необходимо располагать результатами измерений, соответствующими не менее, чем трем уровням фактора. Другими словами, ОДА применяется для анализа не менее трех выборок данных и основан на сравнении их дисперсий. Классический дисперсионный анализ, развитый Р.Фишером, является параметрическим методом: он предполагает, что все выборки взяты из генеральных совокупностей, распределенных по нормальному закону. Для психологических данных это требование часто нарушается, поэтому развиты методы, являющиеся непараметрическими аналогами дисперсионного анализа: для несвязанных выборок это - критерии Краскела-Уоллиса и Джонкира (тема 7.2), а для связанных – критерии Фридмана и Пейджа (тема 8.2). Для применения классического ОДА с формальной точки зрения необходимо выполнение ряда условий: · условие нормальности - эмпирические данные представляют собой случайные выборки (Random samples) из нормально распределенных генеральных совокупностей (Normal population), · условие однородности (гомогенности) дисперсий - выборки имеют равные дисперсии (Equality of group variances – равенство групповых дисперсий, Homogeneity-of-variance – гомогенность дисперсий), · условие независимости: выборки являются независимыми (Independent), т.е. нельзя предсказать значение какого-либо наблюдения по значению другого. На практике допускается нарушение первых двух условий. Обоснованием такой возможности служат результаты, полученные в работах Шеффе, Гласса, Стэнли, Хауэлла и других авторов, показывающие весьма слабую чувствительность дисперсионного анализа к нарушению условия нормальности и выявляющие требования, при которых нарушение условия однородности дисперсий может не учитываться [1. С.13]. В частности, применение ОДА оказывается корректным даже при нарушении условия однородности дисперсий, если выполняются два условия: · объемы выборок равны или отличаются незначительно, · используются выборки большого объема. Нулевой гипотезой ОДА является предположение о равенстве средних рассматриваемых совокупностей; соответственно, альтернативная гипотеза утверждает, что существуют значимые отличия в средних, обусловленные воздействием рассматриваемого фактора. Статистика критерия, которая называется
Эта формула выражает отношение двух дисперсий: межгрупповой На практике при расчетах по методу ОДА важную роль играет сумма квадратов отклонений SS (от англ. «sums of (deviation) squares»), так как именно через подобные суммы рассчитываются дисперсии, входящие в формулу (10.1-1). Точнее говоря, каждая из этих дисперсий вычисляется, как отношение соответствующей суммы квадратов отклонений к количеству степеней свободы df (от англ. «degrees of freedom») [1. C.18-29; 2. С.182-183]:
где:
где: Вычисление сумм квадратов отклонений «вручную» является весьма трудоемким; необходимые для этого расчетные формулы приведены в [1-3; 9; 10; 21]. Обсуждение различных аспектов однофакторного дисперсионного анализа имеется в следующих работах: · постановка задачи ОДА, его концептуальные основы, разновидности и особенности применения в психологических исследованиях обсуждаются в [1; 2. С.179-195; 3. С.224-245; 13; 14; 21; 23; 27; 28]; · теоретические основы, примеры применения и расчетные формулы приведены в [4; 5; 8; 9; 11; 12; 16-18; 20; 22; 29]; · математические основания рассмотрены в [6; 10; 19; 24]; · технология применения в статистических пакетах обсуждается в следующих работах: для пакета SPSS - [1; 25; 26; 30], для пакета Statistica for Windows – [9. С.490-493], для пакета Stadia – [15]. Задача 10.1-1. Применение однофакторного дисперсионного Условие: в торговую фирму пригласили психолога-консультанта, в задачи которого входило изучение стратегий поведения сотрудников фирмы в конфликтных ситуациях, выявляемых с помощью опросника К.Томаса. В частности, исследовалось влияние уровня образования на такие стратегии; при этом рассматривались следующие уровни образования: 1 – среднее (полное и неполное), 2 – среднее специальное, 3 – высшее. Полученные результаты приведены в табл. 10.1-1 (заметим, что показатели должностного статуса в данной задаче не используются: они потребуются в задаче 10.2-1). Найти: можно ли утверждать, что фактор принадлежности к определенной группе по уровню образования влияет на выбор стратегии поведения в конфликте, и, если – да, каков уровень этого влияния для каждой стратегии? Таблица 10.1-1 Показатели образования, должностного статуса
Продолжение табл. 10.1-1
Решение: 1. Выдвигаем гипотезы о влиянии фактора принадлежности к определенной группе по уровню образования на выбор стратегии поведения в конфликте: 2. Применим для решения задачи пакет SPSS. Запускаем пакет и вводим исходные данные, используя переменную var00001 для записи фактора (уровня образования испытуемых), принимающего значения от 1 до 3. В последующие пять колонок таблицы записываем данные по стратегиям поведения в конфликте (переменные var00002, var00003, var00004, var00005, var00006). 3. Вначале необходимо выполнить проверку нормальности распределений переменных var00002-var00006, которая описана при решении задачи 7.1-2. Выполнив шаги 2-5 из решения этой задачи, в окне SPSS Viewer (Просмотр результатов) находим таблицу Tests of Normality (Критерии нормальности). В силу небольшого объема исследуемых выборок более корректным является использование критерия Шапиро-Уилка (а не Колмогорова-Смирнова). Из полученных данных следует, что по этому критерию все исследуемые переменные имеют распределение, не отличающееся от нормального на уровне значимости 0,05. 4. Хотя, как отмечалось в теоретическом разделе, дисперсионный анализ применим и в некоторых случаях нарушения нормальности, однако здесь это не понадобилось: наши данные соответствуют нормальному закону. Теперь мы можем применить однофакторный дисперсионный анализ. Для этого в главном меню программы последовательно выбираем команды: Statistics (Статистики) – Compare means (Сравнение средних) - One-Way ANOVA (Однофакторный дисперсионный анализ). 5. В окне однофакторного дисперсионного анализа в поле Dependent list (Перечень зависимых переменных) задаем исследуемые переменные var00002-var00006, а в поле Factor (Фактор) заносим независимую переменную var00001. 6. Нажимаем кнопку Options (Параметры) и устанавливаем флажок в поле Homogeneity-of-variance (Гомогенность дисперсии), задавая тем самым проверку однородности дисперсии. Нажимаем на кнопку Continue (Продолжить) и возвращаемся вокно One-Way ANOVA (Однофакторный дисперсионный анализ). 7. Выполняем саму проверку и переходим в окно SPSS Viewer (Просмотр результатов). Вначале убеждаемся, что согласно критерию однородности дисперсий для всех исследуемых переменных дисперсии по группам однородны. Для этого просматриваем результаты таблицы Test of Homogeneity of Variances (Проверка гомогенности дисперсий) и видим, что минимальный уровень значимости встречается у переменной var00002 и составляет 0,167. Это дополнительно подтверждает корректность применения к нашим данным однофакторного дисперсионного анализа. Далее в таблице ANOVA находим результаты однофакторного дисперсионного анализа, в частности, следующие:
var00002 0,185 0,834 Отсюда следует, что влияние фактора (уровня образования) имеется для переменных var00003 (Сотрудничество) и var00005 (Приспособление), а для остальных переменных отсутствует. Ответ: фактор принадлежности к определенной группе по уровню образования влияет на выбор двух стратегий поведения в конфликте: сотрудничества и приспособления. Дата добавления: 2015-01-18 | Просмотры: 1663 | Нарушение авторских прав |
 – статистикой Фишера, вычисляется по формуле [1. С.22]:
– статистикой Фишера, вычисляется по формуле [1. С.22]: . (10.1-1)
. (10.1-1) (от англ. between-groups variability - межгрупповая дисперсия) и внутригрупповой
(от англ. between-groups variability - межгрупповая дисперсия) и внутригрупповой  (от англ. within-group variability – внутригрупповая дисперсия). При этом предполагается, что внутригрупповая дисперсия обусловлена случайными причинами, а воздействие рассматрвиаемого фактора проявляется в наличии межгрупповой дисперсии.
(от англ. within-group variability – внутригрупповая дисперсия). При этом предполагается, что внутригрупповая дисперсия обусловлена случайными причинами, а воздействие рассматрвиаемого фактора проявляется в наличии межгрупповой дисперсии. , (10.1-2)
, (10.1-2) - сумма квадратов отклонений, соответствующая
- сумма квадратов отклонений, соответствующая - количество степеней свободы для
- количество степеней свободы для - количество градаций (уровней) фактора,
- количество градаций (уровней) фактора, , (10.1-3)
, (10.1-3) - количество степеней свободы
- количество степеней свободы - общее (суммарное) число наблюдений (измерений,
- общее (суммарное) число наблюдений (измерений,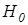 - об его отсутствии,
- об его отсутствии, 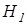 - об его наличии.
- об его наличии.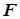 Sig
Sig