 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Ранговая корреляция
Как мы уже знаем, данные в психологических исследованиях относительно редко распределены по нормальному закону. В силу этого использование для выявления связи между переменными коэффициента Пирсона часто является некорректным и, соответственно, возрастает роль непараметрических мер связи, среди которых наиболее популярны различные ранговые коэффициенты корреляции, выявляющие связь между переменными не непосредственно, а косвенно – через определение связи между рядами рангов, соответствующих этим переменным. Среди таких ранговых коэффициента корреляции наиболее популярным является коэффициент Спирмена. Ранговый коэффициент корреляции Спирмена (Spearman correlation coefficient – коэффициент корреляции Спирмена, показатель ранговой корреляции Спирмена, показатель корреляции рангов Спирмена, коэффициент корреляции рангов) применяется в случаях, когда изучается линейная связь между рядами, представленными в количественной или порядковой шкале. Формула для вычисления коэффициента Спирмена [15. C.275] (аналогичные формулы имеются в [2. С.213; 4. С.223]):
где
где Заметим, что многие авторы не используют при вычислении коэффициента Спирмена поправки на объединение рангов [15. С.275], хотя наличие одинаковых рангов означает меньшую степень дифференцированности упорядоченных переменных и, следовательно, меньшую возможность оценить степень связи между ними [31. C.76]. Обсуждение коэффициента ранговой корреляции Спирмена имеется в многочисленных работах: · особенности его применения в психологических исследованиях обсуждаются в [2.С.212-222; 4. С.208-223; 6; 13; 31]; · расчетные формулы и примеры применения приведены в [7; 15; 18; 19; 24; 25]; · математические вероятностно-статистические основания рассмотрены в [8; 12; 14; 17; 20; 22; 27-30; 32-34]; · технология его применения в статистических пакетах обсуждается в следующих работах: для пакета SPSS - [3. С.108-112; 36], для пакета Statistica for Windows – [9. С.502-505], для пакета Stadia – [23]. Задача 9.2-1. Применение корреляции Спирмена для выявления Условие: на выборке школьников проведено исследование с целью проверки наличия взаимосвязи между показателями психологической готовности к вузовскому обучению: умением учиться, навыками самоконтроля, общительностью и успеваемостью (табл. 9.2-1). Найти: установить степень согласованности между данными показателями. Таблица 9.2-1 Показатели психологической готовности
Продолжение табл. 9.2-1
Решение: 1. Применим для решения задачи пакет SPSS. Запускаем пакет и вводим исходные данные в таблицу: по каждой выборке – в отдельный столбец (var00001, var00002, var00003, var00004). 2. В главном меню программы последовательно выбираем команды: Statistics (Статистики) – Correlate (Коррелировать) – Bivariate Correlations (Парные корреляци). 3. В окне парных корреляций задаем исследуемые переменные (var00001, var00002, var00003, var00004), затем устанавливаем флажки в следующие поля: · в разделе Correlation Coefficients (Коэффициенты корреляции) флажком устанавливаем вид коэффициента корреляции - Spearman (Коэффициент Спирмена), · в разделе Test of Significance (Проверка значимости) выбираем тип используемого критерия значимости - Two-tailed (Двухсторонний), · ставим флажок в поле Flag significant correlations (Отметка значимых корреляций). 4. Нажав ОК, выполняем проверку и переходим в окно SPSS Viewer (Просмотр результатов). Выявлены значимые связи: на уровне значимости 0,01 – между var00001 и var00002 ( Ответ: выявлены статистически значимые корреляционные связи между переменными var00001 и var00002, var00002 и var00004, var00001 и var00004. В соответствии с классификацией связей по силе можно утверждать, что связь между var00001 и var00002 является сильной, связь между var00002 и var00004 – средней, а связь между var00001 и var00004 – умеренной. Все остальные связи являются статистически незначимыми (уровень их значимости более 0,05). Вопросы для самопроверки по теме 9 1. Какие меры связи наиболее часто используются для выявления согласованности изменений? 2. В каких пределах может меняться значение коэффициентов корреляции Пирсона и Спирмена? 3. Как классифицируются корреляционные связи по направлению? 4. Как классифицируются корреляционные связи по их силе? 5. В чем различия общей и частной клсссификаций корреляционных связей? 6. Каковы назначение, область применения и ограничения линейного коэффициент корреляцииПирсона? 7. По какой формуле вычисляется коэффициент Пирсона? 8. Каковы назначение, область применения и ограничения рангового коэффициент корреляцииСпирмена? 9. По какой формуле вычисляется коэффициент Спирмена? 10. По какой формуле вычисляются поправки на объединение рангов для коэффициент корреляцииСпирмена? Рекомендуемая литература по теме 9 Дата добавления: 2015-01-18 | Просмотры: 1428 | Нарушение авторских прав |
 , (9.2-1)
, (9.2-1)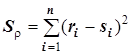 , (9.2-2)
, (9.2-2) - массивы рангов соответственно
- массивы рангов соответственно - поправки на объединение рангов
- поправки на объединение рангов , (9.2-3)
, (9.2-3)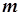 - число групп объединенных рангов в данном ряду;
- число групп объединенных рангов в данном ряду; - число рангов в
- число рангов в  -той группе.
-той группе. = 0,754) и между var00002 и var00004 (
= 0,754) и между var00002 и var00004 (