 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Эмпирические данные по уровню концентрации внимания
Продолжение табл. 6.1-3
Решение: Алгоритм решения аналогичен решению задачи 6.1-1. 1. Выдвигаем гипотезы 2. Запускаем пакет Statistica for Windows, заносим исходные данные в таблицу. Далее выполняем проверку на нормальность. 3. Применяя первый способ, формируем гистограмму эмпирического ряда. Ее визуальный контроль показывает достаточно сильную смещенность вправо, а также островершинность относительно кривой нормального распределения. 4. Применяя второй способ, получаем следующие оценки: 5. Применяя третий способ, замечаем, что объем выборки позволяет применить критерии Колмогорова-Смирнова и Хи-квадрат. Используя приемы из задачи 6.1-1, получаем, что статистика критерия Колмогорова-Смирнова равна 0,173 при Ответ: данные не согласованы с гипотезой нормальности. Дата добавления: 2015-01-18 | Просмотры: 987 | Нарушение авторских прав |
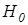 и
и 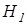 .
.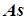 = -1,622;
= -1,622;  = 0,291;
= 0,291; 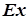 = 2,243;
= 2,243; 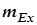 = 0,574. Оценки асимметрии и эксцесса имеют больший порядок, чем их ошибки, что свидетельствует о значимом отличии эмпирического распределения от нормального закона.
= 0,574. Оценки асимметрии и эксцесса имеют больший порядок, чем их ошибки, что свидетельствует о значимом отличии эмпирического распределения от нормального закона. < 0,05; статистика критерия Хи-квадрат равна 81,304 при
< 0,05; статистика критерия Хи-квадрат равна 81,304 при