 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Выявление различий в распределениях признакаДля выявления различий в распределениях признака в двух эмпирических выборках, как и для сравнения с теоретическим распределением, применяются критерии Колмогорова-Смирнова и Хи-квадрат Пирсона, рассмотренные в теме 6.1. Критерий Хи-квадрат имеет множество применений и используется для проверки гипотез независимости, согласия, однородности. Для оценки достоверности отсутствия различий между двумя выборочными распределениями применяют вариант этого критерия, предназначенный для проверки гипотезы однородности. Статистика данного критерия в общем случае (для выборок разного объема) имеет вид [1. С.143; 10. С.123; 12. C.270-283]:
где: Обсуждение критерия Хи-квадрат имеется, в частности, в источниках [1; 3-5; 7-12; 16; 18; 21]. Задача 6.2-1. Сравнение двух эмпирических распределений Условие: с помощью методики «Дифференциальная диагностика депрессивных состояний» В.А.Жмурова определены показатели уровня депрессивных состояний для взрослых испытуемых из выборок, образованных по типам профессий «человек-художественный образ» (выборка A) и «человек-знак» (выборка B). Полученные результаты приведены в табл. 6.2-1. Найти: существуют ли различия в распределениях уровней депрессивных состояний в двух эмпирических выборках? Таблица 6.2-1 Уровни депрессивных состояний для выборок по типам
Решение: 1. Выдвигаем гипотезы: 2. Для решения данной задачи применим пакет SPSS. Запускаем его и в стартовом окне флажком выбираем возможность Type in data (Ввести данные). Появляется новая таблица для ввода данных. 3. Объемы выборок ( 4. В главном меню программы последовательно выбираем команды: Statistics (Статистики) – Nonparametric tests (Непараметрические критерии) – 2 Independent Samples (Две независимые выборки). 5. В открывшемся окне Two-Independent-Samples Tests (Критерии для двух независимых выборок): · задаем в поле Test variable list (Список проверяемых переменных) переменную var00001, · в поле Grouping variable (Группирующая переменная) заносим переменную var00002, · флажком выбираем применяемый для проверки критерий Kolmogorov-Smirnov Z (z -тест Колмогорова-Смирнова). 6. Для группирующей переменной выбираем команду Define groups (Определить группы), устанавливаем значения групп 1 и 2 и нажимаем кнопку Continue (Продолжить). 7. Нажав кнопку ОК, выполняем саму проверку и переходим в окно SPSS Viewer (Просмотр результатов). В таблице Test statistics (Результаты теста) находим значение Kolmogorov-Smirnov Z (Статистика критерия Колмогорова-Смирнова), равное 2,268. При этом в поле Asymp. Sig. (2-tailed) (Асимптотический двухсторонний уровень значимости) показано значение 0,000, что свидетельствует о наличии достоверных различий в эмпирических распределениях, следовательно, гипотеза Ответ: распределения по уровню депрессивных состояний в двух выборках существенно отличаются. Задача 6.2-2. Сравнение двух эмпирических распределений Условие: используем условие задачи 6.2-1. Найти: сравнить эмпирические распределения, применив для выявления различий критерий Хи-квадрат. Решение: 1. Запускаем пакет SPSS и вводим данные из табл. 6.2-1 так, как это описано в решении задачи 6.2-1. 2. В главном меню программы последовательно выбираем команды: Statistics (Статистики) – Summarize (Подытожить) – Crosstabs (Таблицы сопряженности). 3. В открывшемся окне таблиц сопряженности в поле Row(s) (Строки) вводим основную переменную var00001, в которую записаны исходные данные из обеих выборок; в поле Column(s) (Столбцы) вводим группирующую переменную var00002. 4. Выбираем в нижней части окна команду Statistics (Статистики) и флажком выбираем критерий Chi-square (Хи-квадрат). 5. Выполняем проверку и переходим в окно SPSS Viewer (Просмотр результатов). В таблице Chi-Square Tests (Результаты теста Хи-квадрат) в строке Pearson Chi-Square (Хи-квадрат Пирсона) находим Value (Значение) статистики критерия, равное 80,914, и Asymp. Sig. (2-sided) (Асимптотический двухсторонний уровень значимости), равный 0,001. Это свидетельствует о наличии статистически достоверных различий в эмпирических распределениях, следовательно, как и в задаче 6.2-1, гипотеза Ответ: критерий Хи-квадрат, как ранее и критерий Колмогорова-Смирнова, выявил статистически значимые отличия в распределениях эмпирических данных. Вопросы для самопроверки по теме 6 1. Чем обусловлена необходимость проверки на соответствие эмпирических данных нормальному закону распределения? 2. Какие три группы методов проверки на нормальность распределения Вы знаете? 3. Опишите два метода проверки на нормальность распределения, основанные на применении описательной статистики и визуализации. 4. Как определяются показатели асимметрии и эксцесса и их стандартные ошибки? В чем их смысл? 5. Каковы значения показателей асимметрии и эксцесса для нормального распределения? 6. Как оценить соответствие нормальному закону распределения по величине показателей асимметрии и эксцесса? 7. Как оценить соответствие распределения нормальному закону по величине ошибок показателей асимметрии и эксцесса? 8. Какие методы проверки на нормальность распределения,основанные на критериях согласия распределений, Вы знаете? 9. В чем состоит общий подход различных критериев согласия распределений к проверке нулевой гипотезы нормальности? 10. Каковы ограничения известных Вам критериев согласия распределений на объемы исследуемых выборок? Рекомендуемая литература по теме 6 Дата добавления: 2015-01-18 | Просмотры: 1667 | Нарушение авторских прав |
 , (6.2-1)
, (6.2-1) - объемы первой и второй выборок;
- объемы первой и второй выборок; - количество интервалов, разбивающих вариационный ряд;
- количество интервалов, разбивающих вариационный ряд;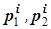 - частоты первого и второго рядов,
- частоты первого и второго рядов, .
.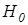 – об отсутствии различий в двух распределениях данных,
– об отсутствии различий в двух распределениях данных, 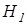 – о наличии таких различий.
– о наличии таких различий. =56) позволяют использовать для сравнения двух эмпирических распределений критерий Колмогорова-Смирнова. Для его применения надо использовать группирующую переменную, поэтому ввод исходных данных в таблицу организуем следующим образом: в первую колонку (var00001) записываем подряд сначала данные первой выборки, указывая для них во второй колонке (var00002) значение группирующей переменной, равное 1, а затем – данные второй выборки, указывая для них во второй колонке значение группирующей переменной, равное 2.
=56) позволяют использовать для сравнения двух эмпирических распределений критерий Колмогорова-Смирнова. Для его применения надо использовать группирующую переменную, поэтому ввод исходных данных в таблицу организуем следующим образом: в первую колонку (var00001) записываем подряд сначала данные первой выборки, указывая для них во второй колонке (var00002) значение группирующей переменной, равное 1, а затем – данные второй выборки, указывая для них во второй колонке значение группирующей переменной, равное 2.