 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Индивидуальные значения показателей фактора «Сила Я»
Решение: 1. Выдвигаем гипотезы: 2. Применим для решения задачи пакет SPSS. Запускаем его и вводим исходные данные, аналогично задаче 6.2-1, используя для обеих выборок одну и ту же переменную var00001 и применяя группирующую переменную var00002, принимающую значение 1 для выборки А и значение 2 для выборки В. 3. В главном меню программы выбираем команды: Statistics (Статистики) – Nonparametric tests (Непараметрические критерии) – 2 Independent Samples… (Две независимые выборки). 4. В открывшемся окне Two-Independent-Samples Tests (Критерии для двух независимых выборок): · задаем в поле Test variable list (Список проверяемых переменных) переменную var00001, · в поле Groupping variable (Группирующая переменная) заносим переменную var00002, · флажком выбираем применяемый для проверки критерий Mann-Whitney U test (U -тест Манна-Уитни). 5. Для группирующей переменной выбираем команду Define groups (Определить группы), устанавливаем значения групп 1 и 2 и нажимаем кнопку Continue (Продолжить). 6. Выполняем саму проверку и переходим в окно SPSS Viewer (Просмотр результатов). В таблице Test statistics (Результаты теста) находим поле Mann-Whitney U, содержащее значение статистики критерия Манна-Уитни: Ответ: статистически значимые различия между выборками отсутствуют. Задача 7.1-2. Применение критерия Стьюдента для выявления Условие: исследован уровень субъективной удовлетворенности организацией учебного процесса среди студентов первого (выборка A) и пятого (выборка B) курсов (табл. 7.1-2). Найти: существуют ли статистически значимые различия между уровнями удовлетворенности в этих выборках? Таблица 7.1-2 Показатели субъективной удовлетворенности
Решение: 1. Выдвигаем гипотезы: 2. Применим для решения задачи пакет SPSS. Запускаем его и, ориентируясь на необходимость проверки нормальности распределений, вначале вводим исходные данные по каждой выборке в отдельный столбец, т.е. в свою переменную - var00001 для первой выборки и var00002 - для второй. 3. Далее необходимо выполнить проверку нормальности распределения для каждой выборки. Для этого в главном меню программы последовательно выбираем команды: Statistics (Статистики) – Summarize (Подытожить) – Explore… (Исследовать). 4. В поле Dependent list (Зависимая переменная) задаем переменные var00001 и var00002, нажимаем кнопку Plots… (Графики)и устанавливаем флажок в поле Normality plots with tests (Графики с критериями для проверки нормальности). Затем нажимаем кнопку Continue (Продолжить). 5. В окне Explore (Исследовать) нажимаем кнопку ОК, тем самым выполнив саму проверку на нормальность, и переходим в окно SPSS Viewer (Просмотр результатов). В таблице Tests of Normality (Критерии нормальности) приведены значения: · для теста Колмогорова-Смирнова: по переменной var00001 – Statistic (Статистика) 0,133, Sig. (Значимость) 0,200; по var00002 статистика равна 0,173 при значимости 0,200; · для теста Шапиро-Уилка: по переменной var00001 - статистика равна 0,980 при значимости 0,961,по переменной var00002 статистика 0,953 при значимости 0,671. Хотя и тот и другой критерий подтверждает нормальность распределений, но более корректным в данном случае является использование критерия Шапиро-Уилка, так как исследуемые выборки имеют небольшой объем (см. тему 6.1). 6. Теперь, после проверки нормальности, мы можем использовать критерий Стьюдента, но для этого надо записать данные выборок в один общий столбец (например, var00001) используя группирующую переменную var00002 со значением 1 для первой выборки, и 2 – для второй. Выполним это, применяя приемы редактирования данных, рассмотренные в теме 5.1. Затем в главном меню программы последовательно выбираем команды: Statistics (Статистики) – Compare means (Сравнение средних) – Independent Samples T Test… ( 7. В открывшемся окне 8. Нажав на кнопку Define groups (Определить группы), устанавливаем для группирующей переменной значения 1 и 2, соответствующие группам и нажимаем Continue (Продолжить). 9. Нажав кнопку ОК, выполняем проверку и переходим в окно SPSS Viewer (Просмотр результатов). В таблице Independent Samples Test (Тест для независимых выборок) в разделе t-test for Equality of Means (t-тест для равенства средних) находим значение статистики критерия Стьюдента Ответ: статистически значимые различия между уровнями удовлетворенности в выборках отсутствуют. Дата добавления: 2015-01-18 | Просмотры: 928 | Нарушение авторских прав |
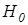 – об отсутствии различий по выборкам в средних значениях показателя «Сила Я»,
– об отсутствии различий по выборкам в средних значениях показателя «Сила Я», 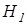 – о наличии таких различий.
– о наличии таких различий. = 70,0. При этом Asymp. Sig. (2-tailed) (Асимптотический двухсторонний уровень значимости) равен 0,781, что свидетельствует об отсутствии достоверных различий в средних значениях двух выборок, значит, мы не имеем оснований отвергнуть нулевую гипотезу
= 70,0. При этом Asymp. Sig. (2-tailed) (Асимптотический двухсторонний уровень значимости) равен 0,781, что свидетельствует об отсутствии достоверных различий в средних значениях двух выборок, значит, мы не имеем оснований отвергнуть нулевую гипотезу  -критерий для независимых выборок).
-критерий для независимых выборок).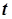 = 0,525, а в поле Sig. (2-tailed) (Значимость двухсторонняя) - уровень значимости 0,606 в обоих вариантах: когда предполагается и когда не предполагается равенство дисперсий (Equal variances assumed и Equal variances not assumed). Это свидетельствует в пользу гипотезы
= 0,525, а в поле Sig. (2-tailed) (Значимость двухсторонняя) - уровень значимости 0,606 в обоих вариантах: когда предполагается и когда не предполагается равенство дисперсий (Equal variances assumed и Equal variances not assumed). Это свидетельствует в пользу гипотезы