 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Сравнение трех и более выборокДля сравнения нескольких (более двух) выборок популярен Статистика критерия Краскела-Уоллиса вычисляется по формуле [1. С.115; 3. С 59; 14. С.179]:
где
Обсуждение критерия Краскела-Уоллиса имеется в работах [1; 3; 4; 14; 19-21; 26; 27; 30; 32]; методика его использования в статистическом пакете SPSS рассмотрена в [2. C.99-101; 35], а в пакете Statistica for Windows – в [9. C.512-516]. Иногда важен не только факт наличия различий в нескольких выборках, но и направление изменения (возрастания или убывания) различий при переходе от выборки к выборке. Для решения таких задач применяется Статистика критерия вычисляется по формуле [14. C.181]:
где
Критерий Джонкира обсуждается в работах [1; 3; 14; 30; 32]; методика его использования в статистическом пакете SPSS рассмотрена в [2. C.100-102; 35], а в пакете Stadia – в [19]. Задача 7.2-1. Применение критерия Краскела-Уоллиса для Условие: в исследовании принимали участие студенты университета. С помощью методики «Стили конфликтного поведения» К.Томаса выявлен уровень выраженности конфликтного поведения (СП - соперничество, СТ - сотрудничество, КП - компромисс), а также с помощью методики Дж.Роттера выявлен уровень субъективного контроля (экстернальность-интернальность). Результаты для группы экстерналов приведены в табл. 7.2-1. Найти: можно ли утверждать, что существуют различия в группе экстерналов по таким показателям стилей конфликтного поведения, как соперничество, сотрудничество и компромисс? Таблица 7.2-1 Показатели выраженности конфликтного
Решение: 1. Выдвигаем гипотезы: 2. Для решения данной задачи применим пакет SPSS. Запускаем пакет, выбрав флажком в стартовом окне возможность Type in data (Ввести данные), последовательно вводим в первую колонку таблицы (переменная var00001) данные всех трех выборок. 3. Во вторую колонку (переменная var00002) заносим значения группирующей переменной: 1 – для первой выборки, 2 – для второй, 3 – для третьей. 4. В главном меню последовательно выбираем команды: Statistics (Статистики) – Nonparametric tests (Непараметрические критерии) – K Independent Samples… (k независимых выборок). 5. В окне критериев для нескольких независимых выборок задаем проверяемую переменную (var00001), группирующую переменную (var00002) и флажком выбираем применяемый для проверки Kruskal-Wallis H ( 6. Для группирующей переменной var00002 выбираем команду Define range (Определить метки групп), устанавливаем пределы значений меток групп от 1 до 3 и нажимаем Continue (Продолжить). 7. Нажав ОК, выполняем проверку и переходим в окно SPSS Viewer (Просмотр результатов). В таблице Test statistics (Результаты теста) находим поле Chi-Square (Хи-квадрат), в котором приведено значение статистики критерия Краскела-Уоллиса Ответ: по полученным данным нельзя утверждать, что существуют статистически достоверные отличия в группе экстерналов по показателям стилей конфликтного поведения. Задача 7.2-2. Применение критерия Джонкира для выявления Условие: для подтверждения гипотезы о возрастании уровня тревожности в синильном и пресинильном возрасте обследованы испытуемые разного возраста: 1-я группа – 20-23 года, 2-я группа – 25-35 лет, 3-я группа – 70-75 лет. Результаты измерений по личностной шкале проявлений тревоги представлены в табл. 7.2-2. Найти: можно ли утверждать, что разные возрастные группы различаются по уровню личностной тревожности? Таблица 7.2-2 Показатели личностной тревожности
Решение: 1. Выдвигаем гипотезы: 2. Применяем для решения задачи пакет SPSS. Сначала надо проверить, упорядочены ли выборки по возрастанию. Для этого, запустив пакет, вводим данные по выборкам в отдельные столбцы (переменные var00001, var00002, var00003). Затем в главном меню программы последовательно выбираем команды: Statistics (Статистики) – Summarize (Подытожить) – Descriptives (Описательные статистики). В открывшемся диалоговом окне задаем исследуемые переменные и, нажав ОК, в окне просмотра результатов получаем следующие значения средних по выборкам: 16,167 - для первой, 33,167 – для второй, 44,333 – для третьей. Таким образом, выборки действительно упорядочены, иначе их пришлось бы соответствующим образом поменять местами. 3. Теперь, аналогично решению задачи размещаем данные из всех трех выборок в первой колонке (переменная var00001), а во вторую колонку (переменная var00002) заносим значения группирующей переменной: 1 – для первой выборки, 2 – для второй, 3 – для третьей. 4. В главном меню программы последовательно выбираем команды: Statistics (Статистики) – Nonparametric tests (Непараметрические критерии) – K Independent Samples… (k независимых выборок). 5. В окне критериев для нескольких независимых выборок задаем проверяемую переменную (var00001), группирующую переменную (var00002) и флажком выбираем применяемый для проверки критерий Jonckheere-Terpstra (Джонкира-Терпстра). 6. Для группирующей переменной var00002 выбираем команду Define range (Определить метки групп), устанавливаем пределы значений меток групп от 1 до 3 и нажимаем Continue (Продолжить). 7. Нажав ОК, выполняем проверку и переходим в окно SPSS Viewer (Просмотр результатов). В таблице Jonckheere-Terpstra Test (Тест Джонкира-Терпстра) видим, что эмпирическое значение статистики критерия, показанное в поле Observed J-T Statistic (Наблюдаемая статистика), равно 103, в то время, как критическое значение статистики критерия, приведенное в поле Mean J-T Statistic (Средняя статистика), равно 54, что соответствует уровню значимости 0,000, показанному в поле Asymp. Sig. (2-tailed) (Асимптотическая двухсторонняя значимость). Этот результат свидетельствует о наличии достоверных различий в распределениях выборок, следовательно, гипотеза 8. Теперь применим для решения данной задачи пакет Stadia. Запускаем пакет и вводим исходные данные в таблицу (каждую выборку – в отдельный столбец). 9. В главном меню программы выбираем команду Статистические методы. 10. В открывшемся окне статистических методов в разделе Дисперсионный анализ выбираем команду Однофакторный. 11. В появившемся окне выбора метода выбираем команду Крускал-Уоллис. На появивишийся запрос «Значения 1-го фактора в выборках упорядочены?» отвечаем «Да» («Yes»). 12. В открывшемся окне просмотра видим следующие результаты: «Джонкхиер = 103» (это значение статистики критерия), «Значимость = 0,01», «Степ. своб. = 3,18» (это показатель степеней свободы). Далее приводится заключение о том, какую гипотезу следует принять: «Гипотеза 1: Есть влияние фактора на отклик». Значит, принимается гипотеза Ответ: степень личностной тревожности возрастает при переходе от группы к группе, осуществляемом в направлении увеличения возраста испытуемых. Вопросы для самопроверки по теме 7 1. В чем заключается основное преимущество и, с другой стороны, основное ограничение параметрических критериев выявления достоверности различий в уровне исследуемого признака по сравнению с непараметрическими? 2. На какие основные группы можно разделить все статистические критерии выявления различий в уровне признака, исходя из количества исследуемых выборок? 3. Какие параметрические критерии выявления достоверности различий в уровне исследуемого признака для двух выборок Вы знаете? 4. Как вычисляется статистика критерия Стьюдента? 5. Каковы назначение, основания и область применения критерия Манна-Уитни? Как вычисляется его статистика? 6. Какие статистические критерии выявления достоверности различий в уровне исследуемого признака для трех и более выборок Вы знаете? 7. Каковы назначение, основания и область применения критерия Крускала-Уоллиса? Как вычисляется его статистика? 8. Каковы назначение, основания и область применения критерия Джонкира? Как вычисляется его статистика? 9. Каковы преимущества и недостатки критерия Джонкира по сравнению с критерием Крускала-Уоллиса? 10. В каких статистических пакетах реализованы статистические критерии выявления достоверности различий в уровне исследуемого признака? Рекомендуемая литература по теме 7 Дата добавления: 2015-01-18 | Просмотры: 5537 | Нарушение авторских прав |
 - критерий Краскела-Уоллиса (Kruskal-Wallis one-way analysis - однофакторный анализ Крускала-Уоллиса, ранговый однофакторный анализ, статистикаКрускала-Уоллиса). Этот критерий является непараметрическим аналогом однофакторного дисперсионного анализа (см. тему 10) и предназначен, в частности, для проверки нулевой гипотезы об одинаковой распределенности всех имеющихся выборок.
- критерий Краскела-Уоллиса (Kruskal-Wallis one-way analysis - однофакторный анализ Крускала-Уоллиса, ранговый однофакторный анализ, статистикаКрускала-Уоллиса). Этот критерий является непараметрическим аналогом однофакторного дисперсионного анализа (см. тему 10) и предназначен, в частности, для проверки нулевой гипотезы об одинаковой распределенности всех имеющихся выборок. , (7.2-1)
, (7.2-1) - сумма рангов наблюдений
- сумма рангов наблюдений  -й группы;
-й группы; - число групп;
- число групп; - общая численность наблюдений.
- общая численность наблюдений. - критерий Джонкира (Джонкхиера, Джонкхиера-Терпстра, Jonckheere-Terpstra test) с альтернативной гипотезой: «различия между выборками существуют, и медианы выборок упорядочены по возрастанию». Для использования этого критерия выборки должны быть упорядочены по предполагаемому возрастанию факторного эффекта (например, средних значений). Как отмечают некоторые авторы, критерий Джонкира позволяет осуществить более детальный анализ и нередко выявляет различия там, где критерий Краскела-Уоллиса показывает отрицательный результат (см., напр., [29]).
- критерий Джонкира (Джонкхиера, Джонкхиера-Терпстра, Jonckheere-Terpstra test) с альтернативной гипотезой: «различия между выборками существуют, и медианы выборок упорядочены по возрастанию». Для использования этого критерия выборки должны быть упорядочены по предполагаемому возрастанию факторного эффекта (например, средних значений). Как отмечают некоторые авторы, критерий Джонкира позволяет осуществить более детальный анализ и нередко выявляет различия там, где критерий Краскела-Уоллиса показывает отрицательный результат (см., напр., [29]). , (7.2-2)
, (7.2-2) - статистика Манна-Уитни для выборок
- статистика Манна-Уитни для выборок ;
;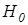 – об отсутствии различий в распределениях данных;
– об отсутствии различий в распределениях данных; 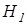 – о наличии таких различий.
– о наличии таких различий. принимается.
принимается.