 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Оценка уровня профессиональной пригодности
Продолжение табл. 6.1-1
Решение: 1. Выдвигаем статистические гипотезы: · · 2. Запустим пакет Statistica for Windows и занесем исходные данные в столбец матрицы данных, соответствующий переменной VAR1. Выполним проверку на нормальность способами, рассмотренными в теоретическом разделе. 3. Применим первый способ проверки на нормальность – с помощью визуальной оценки гистограммы: · В стартовом окне модуля Basic Statistics/Tables (Основные статистики и таблицы) выбираем команду Descriptive Statistics (Описательные статистики). · В поле Variables (Переменные) задаем переменную VAR1, обозначающую уровень профессиональной пригодности. · Выбрав команду Histograms (Гистограмма), строим гистограмму эмпирического ряда, на фоне которой показана теоретическая кривая нормального распределения; визуальный контроль показывает их неплохое соответствие. 4. Применим второй способ проверки на нормальность – с помощью оценок коэффициентов асимметрии и эксцесса: · В окне Descriptive Statistics (Описательные статистики), выбираем команду More statistics (Другие статистики) и устанавливаем флажки против параметров Skewness (Асимметрия), Kurtosis (Эксцесс), Standard errors of the skewness (Стандартная ошибка асимметрии) и Standard errors of kurtosis (Стандартная ошибка эксцесса). · Нажав ОК, возвращаемся в окно Descriptive Statistics (Описательные статистики). После нажатия кнопки ОК появляется таблица, в которой показаны результаты анализа: показатель асимметрии (–0,229) и его ошибка (0,254); показатель эксцесса (–0,300) и его ошибка (0,503). Здесь и далее, во всех решениях задач, результаты округлены до третьего знака после запятой. Оценки асимметрии и эксцесса имеют тот же порядок, что и их ошибки, значит, полученные ненулевые значения оценок асимметрии и эксцесса статистически незначимы и нет оснований отклонить нулевую гипотезу, т.е. эмпирические данные согласованы с гипотезой нормальности. 5. Применим третий способ проверки на нормальность. При этом заметим, что достаточно большой объем выборки ( · Запускаем модуль Nonparametric Statistics & Fitting (Непараметрические статистики и подгонка распределения) и в разделе его стартового окна Continuous distribution (Непрерывное распределение) нажимаем на кнопку Normal (Нормальное). · В поле Variables (Переменные) задаем переменную VAR1 и нажимаем ОК. · Появляется таблица с результатами анализа, в которой статистика критерия Колмогорова-Смирнова равна 0,040, причем данный результат незначим ( · В соответствии с теоретическими положениями о проверке гипотезы на нормальность из этих результатов можно заключить, что альтернативная гипотеза отвергается. Ответ: данные согласованы с гипотезой нормальности. Задача 6.1-2. Проверка на нормальность распределения Условие: среди управленческого персонала частной фирмы исследован уровень волевой регуляции (УВР) (табл. 6.1-2). Найти: соответствуют ли полученные эмпирические данные нормальному закону распределения. Таблица 6.1-2 Дата добавления: 2015-01-18 | Просмотры: 1087 | Нарушение авторских прав |
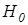 – об отсутствии различий между распределением эмпирических данных и нормальным законом распределения,
– об отсутствии различий между распределением эмпирических данных и нормальным законом распределения,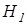 – о наличии таких различий.
– о наличии таких различий. =90) позволяет нам уверенно использовать для проверки на нормальность критерии Колмогорова-Смирнова и Хи-квадрат.
=90) позволяет нам уверенно использовать для проверки на нормальность критерии Колмогорова-Смирнова и Хи-квадрат. = n.s.); статистика критерия Хи-квадрат равна 5,093 при
= n.s.); статистика критерия Хи-квадрат равна 5,093 при