 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Проверка на нормальность распределения
Картина поля заземлителя показана на рис. 13.15. Сопротивление растеканию [12]
III. Проверка статистических гипотез Тема 6. Критерии согласия распределений Проверка на нормальность распределения Во многих ситуациях необходимо выполнять проверку распределения полученной по экспериментальным данным случайной величины на соответствие нормальному закону. В частности, от этого зависит корректность применения параметрических критериев проверки статистических гипотез и некоторых многомерных методов анализа данных (например, дискриминантного или факторного анализа). Методы проверки на нормальность можно разделить на две группы, основанные, соответственно: · на описательной статистике и визуализации, · на критериях согласия распределений. Методы, основанные на описательной 1. Визуальный метод включает построение гистограммы эмпирического распределения (такая возможность реализована во всех популярных статистических пакетах) и ее визуальное сравнение с теоретической кривой нормального распределения.. 2. Оценка показателей асимметрии и эксцесса. Асимметрией (Skewness), или выборочным коэффициентом скошенности, называют меру отклонения эмпирического распределения частот от распределения, симметричного относительно максимальной ординаты [3. С.22; 18. C.11]:
Для симметричных распределений показатель асимметрии равен нулю. Отрицательный показатель асимметрии означает, что кривая распределения скошена влево, положительный – вправо от теоретической симметричной кривой распределения. Стандартная ошибка асимметрии (Standard error of skewness ), или просто - ошибка асимметрии, - это отклонение показателя асимметрии от нуля, которое находится по формуле [10. С.44; 12. C.53]:
Другая характеристика степени отклонения эмпирической кривой распределения от теоретической кривой нормального распределения, - это показатель эксцесса (Kurtosis ), или выборочный коэффициент островершинности [3. С.23; 18. C.11]:
Стандартная ошибка эксцесса (Standard error of kurtosis) может быть вычислена по формуле [10. С.45; 12. C.57]:
Для нормального распределения показатели асимметрии и эксцесса равны нулю:
Для проверки на нормальность иногда применяют следующие соотношения для выборочных коэффициентов асимметрии и эксцесса [13. C.59; 15. C.213]: · распределение считается симметричным, если · распределение считается близким к нормальному, если Кроме того, некоторые авторы рекомендуют следующий прием проверки на нормальность [6. С.132]: · распределение считается близким к нормальному, если вычисленные значения асимметрии и эксцесса имеют тот же порядок, что и их вычисленные ошибки. Методы, основанные на критериях Для проверки на нормальность распределения наиболее часто применяют следующие статистические критерии: 1. Хи-квадрат (Chi-square test, 2. Омега-квадрат ( 3. Колмогорова-Смирнова (Kolmogorov-Smirnov test) [1-4; 18; 20; 21]; 4. Объединяет все эти критерии общий подход к проверке гипотезы нормальности (нулевой гипотезы): а) рассчитывается уровень значимости б) если в) если Наиболее популярен критерий Хи-квадрат, статистика которого для случая сравнения эмпирического распределения с теоретическим вычисляется по формуле [1. C.126; 3. C.124]:
где: Критерии согласия распределений имеют существенные ограничения по объему выборки: · для критерия Хи-квадрат - · для критерия Колмогорова-Смирнова - · для критерия Омега-квадрат - Если эти условия не выполняются, следует применять Далее приводятся задачи, иллюстрирующие применение методов проверки распределения на нормальность. Задача 6.1-1. Проверка на нормальность распределения Условие: при приеме на работу сотрудников страховой компании проведено исследование уровня профессиональной пригодности (УПП) на выборке из 90 человек (табл. 6.1-1). Найти: соответствуют ли полученные эмпирические данные нормальному закону распределения. Таблица 6.1-1 Дата добавления: 2015-01-18 | Просмотры: 3228 | Нарушение авторских прав |
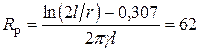 Ом.
Ом. . (6.1-1)
. (6.1-1) . (6.1-2)
. (6.1-2) . (6.1-3)
. (6.1-3) . (6.1-4)
. (6.1-4)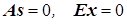 . (6.1-5)
. (6.1-5)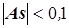 , и сильно асимметричным, если
, и сильно асимметричным, если 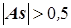 ;
;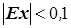 , и значительно отклоняющимся от нормального при
, и значительно отклоняющимся от нормального при 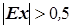 .
.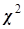 test), или Хи-квадрат Пирсона [1-4; 6; 7; 9-11];
test), или Хи-квадрат Пирсона [1-4; 6; 7; 9-11]; -test), или тест Крамера-Мизеса, Смирнова-Крамера-Мизеса [4; 10; 16; 19];
-test), или тест Крамера-Мизеса, Смирнова-Крамера-Мизеса [4; 10; 16; 19]; -критерий Шапиро-Уилка (Shapiro-Wilks'
-критерий Шапиро-Уилка (Shapiro-Wilks'  , соответствующий полученному значению статистики критерия;
, соответствующий полученному значению статистики критерия; 0,05, то гипотеза о нормальности распределения отклоняется, соответственно принимается гипотеза о наличии значимых отличий от нормальности.
0,05, то гипотеза о нормальности распределения отклоняется, соответственно принимается гипотеза о наличии значимых отличий от нормальности. , (6.1-6)
, (6.1-6) - количество разрядов признака (интервалов,
- количество разрядов признака (интервалов, - порядковый номер разряда признака;
- порядковый номер разряда признака;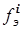 - эмпирическая частота по
- эмпирическая частота по  - теоретическая частота по
- теоретическая частота по 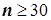 [3. C.117],
[3. C.117], [3. C.143],
[3. C.143],