АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Группировочные признаки

Применение аналитических группировок отличается от других видов вторичной сводки повышенной сложностью, обусловленной не только овладением специальной методики проведения группировки, но и предопределяет обязательное освоение и использование многих вспомогательных методов: относительных, средних величин, вариационных рядов, показателей вариации, выборочного метода и др.

Полученная в результате сплошного или выборочного статистического наблюдения информация обычно содержит разнообразные данные о факторных и результативных признаках, которые характеризуют каждую статистическую единицу. Причинно-следственная вариация признаков в статистической совокупности может служить базой для определения характера и размера изменений результативных признаков в зависимости от колебания факторов.

В целях выявления взаимосвязи между факторными и результативными признаками в статистической совокупности могут быть использованы аналитические группировки. Область их применения очень широка. Аналитические группировки могут находить большое применение при выявлении взаимосвязи между двумя взаимозависимыми признаками и между комплексом взаимосвязанных признаков. Так, с помощью аналитической группировки можно выявить наличие или отсутствие зависимости урожайности культуры от какого-либо одного агротехмероприятия или от комплекса агротехнических мероприятий. Если по каждому хозяйству известна, допустим, урожайность пшеницы и использованные разнообразные агротехнические мероприятия, то группируя эти данные по величине какого-либо одного агротехмероприятия, можно проследить за изменением урожайности, связанной с вариацией этого мероприятия. Именно таким образом может быть выявлено влияние только одного агротехмероприятия.

Гораздо сложнее обстоит дело с выявлением влияния комплекса агротехнических мероприятий на урожайность пшеницы. Решение этого вопроса возможно на основе применения сложной (комбинированной) группировки, которая включает в одновременную разработку не одно, а несколько агротехмероприятий, совместно предопределяющих изменение урожайности.

Таким образом, аналитические группировки дают возможность выявить наличие или отсутствие связи между факторными и результативными признаками в статистической совокупности. При этом целесообразно обратить внимание на то, что в статистике зависимые признаки принято называть результативными, а признаки, оказывающие влияние на них, – факторными. Например, во взаимосвязи доз удобрений и урожайности культур, безусловно, первый признак (дозы удобрений) – факторный, второй (урожайность) – результативный.

Применение аналитических группировок неизбежно связано с группировочным признаками, которые принимаются за основу формирования групп в процессе проведения статистической группировки. Группировочные признаки принято называть основанием группировки. В качестве основания группировки обычно принимают факторные признаки. Вместе с тем в некоторых случаях за основание могут быть взяты и результативные признаки, так как не всегда можно отчетливо разграничить между собой признаки-факторы и признаки-результаты. Например, во взаимосвязи производительности и оплаты труда сложно определить, какой из этих признаков факторный, а какой – результативный. С одной стороны производительность труда – определяющий признак, от которого непосредственно зависит оплата труда, т.е. только ее с ростом возможно повышение оплаты. Но с другой стороны, не следует забывать о том, что без роста оплаты труда невозможно достичь повышения уровня его производительности.

Выбор группировочных признаков в значительной степени определяет результаты аналитической группировки и выводы, которые могут быть сформулированы на основе этих результатов. Роль, значимость факторных и результативных признаков может меняться: в одной взаимосвязи какой-то признак может выступать в качестве результативного, в другой – факторного. Например, урожайность сельскохозяйственных культур, являясь результатом влияния на нее комплекса агротехмероприятий, в то же время во взаимосвязи с себестоимостью единицы продукции становится факторным признаком. Себестоимость, безусловно, признак-фактор по отношению, например, к уровню рентабельности продукции. Поэтому иногда в качестве группировочных могут быть использованы и результативные признаки.

Аналитические группировки в большинстве случаев проводятся по существенным количественным признакам. Вместе с тем нередко возникает необходимость применения такой аналитической группировки, основание которой может сочетать количественные признаки с качественными.

Метод аналитических группировок позволяет не только выявить наличие или отсутствие взаимосвязи между признаками, но и определить факторы, влияющие на эту связь. Это означает, что аналитическая группировка помогает установить причину изменения результативных признаков под воздействием признаков-факторов. Таким образом, достоверное знание причинно-следственной связи между признаками в статистической совокупности позволяет воздействовать на факторные признаки и тем самым управлять процессами формирования результативных признаков в нужном направлении.

Целесообразно обратить внимание на то, что при выборе признаков для проведения аналитической группировки необходим осторожный и критический подход. Это относится как к факторным, обычно группировочным, так и к результативным признакам. Неправильный выбор признаков для основания группировки и ее результатов может привести к грубым ошибкам и необоснованным выводам.

Важнейшее требование, которое предъявляется к аналитическим группировкам, заключается в достаточной представительности генеральной или выборочной совокупности. Как правило, аналитическая группировка по малой выборке не проводится, так как при этом статистические характеристики в некоторых группах с малой частотой, (менее 5 единиц) оказываются смещенными (несостоятельными, недействительными) и, следовательно, не репрезентативны.

Содержание и значение комбинированной группировки

При факторном анализе с помощью метода аналитических группировок можно использовать прием комбинированной (сложной) группировки, которая по существу является продолжением простой аналитической группировки.

Комбинированная группировка – прием проведения аналитической группировки, где в качестве основания принимается сочетание не менее двух существенных группировочных признаков. Комбинированные аналитические группировки могут проводиться, главным образом, по количественным признакам, хотя в некоторых случаях за основание группировки принимают сочетание качественных и количественных признаков. Например, при факторном анализе уровня жизни все население прежде всего подразделяется на группы по качественным признакам (полу, типу населенных пунктов, виду занятий, источникам средств существования), а затем – по количественным признакам (размеру зарплаты, социальных льгот, доходам от личного подсобного хозяйства, расходам на питание, жилье, социальное страхование, медицинское обслуживание и т.д.).

Основная цель комбинированной группировки заключается в выявлении взаимосвязи между несколькими существенными группировочным и результативными признаками. Кроме того, прием комбинированной группировки позволяет определить факторы, формирующие сложные причинно-следственные связи.

Последовательность проведения комбинированной аналитической группировки принципиально не отличается от приема построения простой группировки. Для этого в начале необходимо определить существенные группировочные признаки, которые будут служить основанием комбинированной группировки. Затем формирует интервальные группы по первому группировочному признаку, далее выделенные группы подразделяются на подгруппы по второму группировочному признаку. Выделенные подгруппы целесообразно разделить на подгруппы по следующему признаку и т.д.

Общее число групп и подгрупп, которое может быть сформировано в процессе проведения приема комбинированной группировки, ориентировочно рассчитывают по формуле

, (3.1)

где N – общее число групп и подгрупп; К – число групп (подгрупп) по каждому группировочному признаку; m – число группировочных признаков в комбинированной группировке.

Из формулы 3.1 следует, что с увеличением количества группировочных признаков общая численность групп и подгрупп в комбинированной группировке прогрессивно возрастает. По каждой группе или подгруппе должен быть обеспечен надежный уровень представительности по числу входящих в нее статистических единиц. Если исходить из теории выборочного метода, то можно утверждать, что минимальный уровень представительности каждой подгруппы может быть достигнут при условии, если в подгруппу войдет не менее 5 статистических единиц. В этом случае точечная оценка основных статистических характеристик по результативным признакам группировки начинает приближаться к состоятельной.

Одна из важнейших особенностей применения приема комбинированной группировки – привлечение повышенного числа статистических единиц в составе генеральной или выборочной совокупности. Расчеты показывают, что если сформировать минимальное число групп (3) и подгрупп (3) по двум группировочным признакам, то общая численность групп и подгрупп в комбинированной группировке составит 9, а теоретически необходимое минимальное число статистических единиц равно 45; по трем группировочным признакам – 135, по четырем — 405 единиц. Это только минимум. С учетом же действия закона нормального распределения необходимое число статистических единиц для проведения комбинированной группировки существенно возрастает. Поэтому прием аналитической комбинированной группировки по 3 – 4 и более группировочным признакам сравнительно редкий.

Комбинированная группировка позволяет улучшить аналитичность взаимосвязей между признаками, способствует углубленному изучению массовых явлений. Это бесспорное преимущество приема комбинированных группировок по сравнения с простыми группировками может быть обеспечено при условии достаточно большой выборки единиц в статистической совокупности. Дело в том, что достаточная представительность каждой группы и подгруппы способствует выравниванию (нивелированию) количественных различий между статистическими единицами по многочисленным признакам. С помощью именно такого приема достигается элиминирование комплекса неучтенных факторов при проведении аналитических группировок.

Вариационные ряды

Вариационный ряд представляет собой расположение значений признака каждой статистической единицы в определенном порядке. При этом отдельно взятые значения признака принято называть вариантой (вариантом).. Каждый член вариационного ряда (варианта) называется порядковой статистикой, а номер варианты — рангом (порядком) статистики. Важнейшими характеристиками вариационного ряда являются его крайне варианты (х₁ =х _min; х_n =х _max) и размах вариации (R_х = х_n – х₁).

Вариационные ряды широко применяются при первичной обработке статистической информации, полученной в результате статистического наблюдения. Они служат базой для построения эмпирической функции распределения статистических единиц в составе статистической совокупности. Поэтому вариационные ряды называют рядами распределения.

В статистике различает следующие виды вариационных рядов: ранжированный, дискретный, интервальный.

Ранжированный (от латинского rang – чин) ряд – это такой ряд распределения единиц статистической совокупности, в котором варианты признака размещены в порядке возрастания или убывания. Любой ранжированный ряд состоит из ранговых номеров (от 1 до n) и соответствующих им вариант. Их число в ранжированном ряду, сформированному по существенному признаку, обычно равно числу единиц в статистической совокупности.

Для формирования ранжированного ряда по заданному признаку (например, по числу работников животноводства в 100 сельскохозяйственных организациях) можно воспользоваться макетом табл. 3.5.

Ранжированный ряд имеет как преимущества, так и недостатки. Основное его преимущество в том, что каждая варианта ряда занимает строго определенное место в статистической совокупности, а главный недостаток состоит в громоздкости ранжированного ряда, особенно в том случае, если совокупность включает многие тысячи статистических единиц.

Т а б л и ц а 3.5. Порядок формирования ранжированного ряда по числу работников животноводства

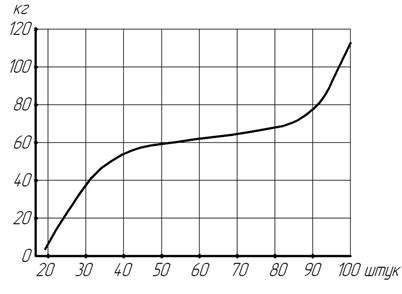
Формирование ранжированного ряда обычно вызвано необходимостью размещения каждой статистической единицы в строго определенном порядке по одному, двум, трем и более признакам. Например, ранжирование сельскохозяйственных, перерабатывающих организаций по размеру ирезультатам производства продукции; ранжирование стран мира по рейтингу экономического развития.

Характер изменения вариант по заданному признаку в статистической совокупности наглядно можно представить при графическом представлении ранжированного ряда с помощью линейной диаграммы. При этом в системе координат на оси абсцисс (ОХ) размещают независимую переменную – ранговые номера (№) ряда, на оси ординат – варианты, соответствующие каждому ранговому номеру (№). Полученная кривая линия называется огивой Гальтона (рис. 3.1).

Рис. 3.1. Изменение средней живой массы свиней на свиноводческих фермах (огива Гальтона)

Характерная особенность огивы заключается в том, что начальная и конечная части кривой линии относительно невелики и выделяются повышенной крутизной подъема, середина же занимает основную часть диаграммы и отличается сравнительной плавностью перехода от варианты к варианте. Это указывает на то, что в достаточно большой статистической совокупности основная масса единиц обычно тяготеет к середине ранжированного ряда.

Ранжированный ряд используется при расчёте и оценке средних величин и показателей вариации. Использование ранжированного ряда и его огивы позволяет анализировать характер распределения. Для перехода к более совершенной форме описания вариации применяют другие виды рядов распределения.

Дискретный (разделенный) ряд – это такой вариационный ряд, в котором его группы сформированы по признаку, изменяющемуся прерывно, т.е. через определённое число единиц. Обычно его формируют по вариантам прерывного (дискретного) признака. В особых случаях, когда имеется целесообразность сформировать дискретный ряд по непрерывному признаку, варианты этого признака приходится округлять.

Общая схема дискретного ряда может быть следующей: некоторая переменная х (варьирующий признак) принимает различные значения х₁, х₂, х₃,…..х_п и имеет соответствующую локальную частоту f_1, f ₂, f₃, … f_n. Под ней понимается абсолютное число, показывающее, сколько раз (как часто) встречается в статистической совокупности то или иное значение (варианта) признака или, что то же самое, сколько единиц в совокупности соответствует тем или иным значением признака.

В некоторых случаях локальные частоты могут быть заменены локальными частостями. В отличие от частот это структурные относительные показатели, определяющие долю локальных частот по каждой варианте в общей сумме частот. При этом частости могут выражаться в долях единицы, либо в процентах.

В дискретном ряду распределения могут быть предусмотрены накопленные частоты или частости, которые исчисляются путем последовательного суммирования к частоте (частости) первой варианты ряда частот (частостей) последующих вариант дискретного ряда. Накопленные частоты (частости) показывают, сколько единиц совокупности или какая их доля не превышает данную варианту в составе ряда. При формировании дискретного (разделенного) ряда рекомендуется воспользоваться макетом табл. 3.6.

Т а б л и ц а 3.6. Порядок формирования дискретного ряда по числу

Дата добавления: 2016-06-06 | Просмотры: 688 | Нарушение авторских прав