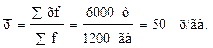|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Средняя арифметическая величина
Если в формулу (6.1) подставить значение к=1, то получается средняя арифметическая величина, т.е.
Поскольку в ранжированном ряду при всех вариантах f=1, то в этом случае применяется средняя арифметическая невзвешенная (простая) величина, т.е.
где n – число единиц в статистической совокупности. Расчет средней арифметической простой можно показать на примере ранжированного ряда, составленного по площади посева льна-долгунца в 20 сельскохозяйственных организациях района (табл. 6.1.).
Т а б л и ц а 6.1. Расчет средней арифметической простой в ранжированном ряду распределения
Подставив данные табл. 6.1 в формулу (6.3), получаем среднее арифметическое простое значение посевной площади льна-долгунца, приходящейся на 1 хозяйство:
Поскольку в дискретном ряду распределения каждая варианта представлена определенной локальной частотой (частостью), то среднее значение для каждого такого ряда можно рассчитать по формуле средней арифметической взвешенной, т.е.
где х – варианты (значение признака); f – локальные частоты (частости). Определение средней арифметической взвешенной величины можно показать на примере расчёта средней урожайности льносоломки в 20 сельскохозяйственных организациях района (табл. 6.2.).
Т а б л и ц а 6.2. Расчет средней арифметической взвешенной в дискретном ряду распределения
Подставив в формулу (6.4) данные табл. 6.2, можно рассчитать среднюю арифметическую взвешенную величину для дискретного ряда распределения:
Таким образом, средняя урожайность, взвешенная по посевной площади льна-долгунца, в сельскохозяйственных организациях района, составила 50 ц/га льносоломки. Принцип расчёта средней величины в интервальном вариационном ряду аналогичен расчёту среднего значения признака для дискретного ряда (формула 6.4); различия состоят лишь в некоторых деталях. При вычислении среднего значения признака в интервальном ряду распределения, когда в столбце вариант имеется не одно, а два значения, показывающие нижнюю и верхнюю границы интервала, прежде всего целесообразно найти его срединное значение, т.е. центр интервала, который определяется как простая средняя арифметическая из нижней и верхней варианты каждого интервала, или как их полусумма. Порядок расчёта средней арифметической взвешенной для интервального вариационного ряда по урожайности льносоломки в сельхозорганизациях с закрытыми интервалами показан в табл. 6.3.
Т а б л и ц а 6.3. Расчёт средней взвешенной варианты в интервальном ряду Дата добавления: 2016-06-06 | Просмотры: 657 | Нарушение авторских прав |
 . (6.2)
. (6.2)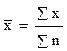 , (6.3)
, (6.3) .
. , (6.4)
, (6.4)