 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Структурные средниеВ некоторых случаях для получения обобщающей характеристики статистической совокупности по какому-либо признаку приходится пользоваться так называемыми структурным средними. К ним относят моду и медиану. Мода представляет собой варианту, наиболее часто встречающуюся в данной статистической совокупности. В ранжированном ряду мода как правило, не определяется, так как каждой варианте соответствует частота, равная единице. Мода в дискретном ряду соответствует варианте с наибольшей частотой, при этом случайная величина может иметь несколько мод. При наличии одной из них распределение статистической совокупности принято называть одномодальным, при наличии двух мод – бимодальным, трех и более мод – мультимодальным. Наличие нескольких мод нередко означает объединение в одной совокупности разнокачественных статистических единиц. Мода для интервального ряда с равными интервалами рассчитывается по формуле
где хмо – нижняя граница модального интервала; iмо – величина интервала; fмо – частота модального интервала; fдмо – частота домодального интервала; fзмо – частота замодального интервала. Допустим, рыночные цены на яблоки по районным центрам области сложились следующим образом (табл. 6.8). По этим данным необходимо рассчитать моду рыночных цен на картофель.
Т а б л и ц а 6.8. Рыночные цены на яблоки
Из данных табл. 6.8 видно, что максимальное число рынков сосредоточено в третьем интервале, причем распределение статистической совокупности унимодальное. Для расчёта моды рыночных цен на яблоки воспользуемся формулой (6.12):
Таким образом, модальная рыночная цена на яблоки в районных центрах области составляет 1690 р/кг. Модальная варианта при характеристике статистической совокупности может быть использована в тех случаях, когда расчёт средней величины затруднен либо невозможен, например, в рыночных условиях при изучении спроса и предложения, уровня цен и т.д. Медиана – варианта, находящиеся в середине вариационного ряда. Медиана в ранжированном ряду находится следующим образом. Во-первых, рассчитывают номер медианой варианты:
где nме – номер медианой варианты; n – общее число вариант в ряду. Во-вторых, в ранжированном ряду определяется значение медианой варианты: если общее число вариант нечетное, то медиана соответствует рассчитанному по формуле (6.13) номеру. Допустим, ранжированный ряд состоит из 99 единиц, распределенных по урожайности сахарной свеклы. Медианный номер варианты находим по формуле (6.13): Это означает, что под № 50 находится искомая медиана урожайности, которая равна, например, 500ц/га. Если же общее число вариант четное, то медиана равна полумсуме двух смежных медианных вариант. Например, в ранжированном ряду имеется 100 статистических единиц, распределенных опять-таки по урожайности сахарной свеклы. Следовательно, в таком ряду имеется два медианных номера, что видно из следующего расчета по формуле (6.13):
Значит, в этом случае медианными считаются № 50 и 51, а медиану урожайности сахарной свеклы, например, можно рассчитать как следующую полусумму двух смежных урожайностей, т.е.
Для дискретного ряда распределения медиану рассчитывают по накопленным частотам: во-первых, находят полусумму накопленных частот; во-вторых, определяют соответствие этой полусуммы конкретной варианте, которая и будет медианой. Например, годовой удой коров распределен в виде дискретного ряда, в котором сумма накопленных частот составляет 200 единиц и, соответственно, полусумма – 100 единиц. Этот медианный номер находится в группе статистических единиц дискретного ряда и соответствует годовому удою коров 5000 кг молока, что и является медианой дискретного ряда. В интервальном вариационном ряду медиану рассчитывают по формуле
где Ме – медиана интервального ряда; хме – нижняя граница медианного интервала; iме – величина медианного интервала; Σf – сумма накопленных частот в интервальном ряду; fн – накопленная частота домедианного интервала; fме – частота медианного интервала. Для расчёта медианы в интервальном ряду воспользуемся следующими данными (табл.6.9).
Т а б л и ц а 6.9. Урожайность картофеля в личных подсобных Дата добавления: 2016-06-06 | Просмотры: 544 | Нарушение авторских прав |
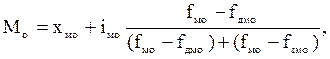 (6.12)
(6.12)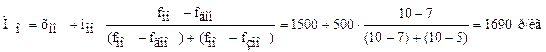
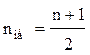 , (6.13)
, (6.13)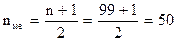 .
.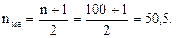
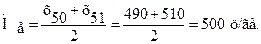
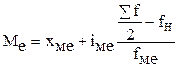 , (6.14)
, (6.14)