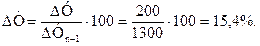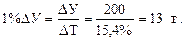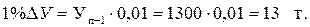|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Абсолютное значение одного процента приростаПри анализе динамических рядов нередко ставится задача: выяснить, какими абсолютными значениями выражается 1 % прироста (снижения) уровней, так как в ряде случаев при снижении (замедлении) темпов роста абсолютный прирост может возрастать. В связи с этим возникает необходимость в расчете абсолютного значения одного процента прироста (снижения). Абсолютное значение одного процента прироста представляет собой отношение абсолютного прироста к темпу прироста, выраженному в процентах:
где 1 % ΔУ – абсолютное значение 1 % прироста; ΔУ – абсолютный прирост уровня; ΔТ – темп прироста, %. После несложного преобразования формулы (10.16) получим, что
Это означает, что абсолютное значение 1 % прироста (снижения) равно 0,01 предыдущего уровня. Например, известно, что объем выпуска яблочного сока в перерабатывающей организации за 2008 г. составил 1300 т, за 2010 г.–– 1500 т. Необходимо определить абсолютное значение 1 % прироста объема продукции в 2010 г. по отношению к 2008 г. Для расчета искомого показателя прежде всего найдем абсолютный прирост объема продукции в 2010 г. (1500-1300=200),а затем рассчитаем темп прироста продукции за этот же период:
Далее можно найти абсолютное значение 1 % прироста по выпуску яблочного сока:
К такому же результату приходим, рассчитав абсолютное значение 1 % прироста продукции более коротким путем:
Комплексное оформление результатов расчета основных показателей динамического ряда обычно проводится с помощью статистической таблицы. Например, при изучении пятилетней динамики урожайности озимого рапса в сельскохозяйственной организации «Днепр»были получены следующие результаты (табл. 9.6).
Т а б л и ц а 9.6. Основные показатели динамики урожайности Озимого рапса
Данные табл. 9.6 показывают, что для динамики урожайности озимого рапса в сельскохозяйственной организации за изучаемый период характерно снижение текущих уровней по сравнению с начальным (базисным) уровнем. Однако, начиная с серединного уровня, урожайность рапса постепенно повышалась, о чем свидетельствуют цепные темпы роста и прироста. Таким образом, для изучаемого динамического ряда характерна гиперболическая форма развития уровней.
Дата добавления: 2016-06-06 | Просмотры: 579 | Нарушение авторских прав |
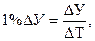 (9.16)
(9.16)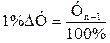 . (9.17)
. (9.17)