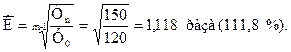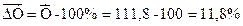|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Темпы прироста уровнейЕсли абсолютная скорость прироста уровней динамического ряда характеризуется величиной абсолютных приростов, то относительная скорость прироста уровней – темпами прироста. Темп прироста представляет собой отношение абсолютного прироста к уровню, принятому за базу. Темпы прироста, как и темпы роста, могут быть выражены в форме коэффициентов и процентов. Коэффициент прироста показывает, на какую долю увеличился или уменьшился последующий уровень по сравнению с предыдущим, т.е.
где ΔК – коэффициент прироста уровня, выраженный в долях; ΔУi – абсолютный прирост уровня; Уi-1 – предыдущий уровень. Темп прироста, выраженный в процентах, показывает, на сколько процентов увеличился или уменьшился последующий уровень по сравнению с предыдущим, т.е.
Пример. Валовой сбор семян многолетних трав во всех категориях хозяйств административного района составил: в 2009 г. – 45 т, в 2010 г. – 48 т. Необходимо найти темп прироста сбора семян в 2010 г. по сравнению с 2009 г. Для решения прежде всего найдем абсолютный прирост уровней:
Темпы прироста также, как и темпы роста, могут быть рассчитаны базисным и цепным способами. Между темпами прироста и темпами роста существует непосредственная связь. Поэтому коэффициент (темп) прироста можно выразить через темп роста, т.е.
Это означает, что коэффициент прироста всегда на единицу меньше соответствующего коэффициента роста. Если же темп прироста выражен в процентах, то он на 100 процентных пунктов меньше темпов роста. Допустим, если темп роста урожайности зерновых культур составил 118 %, то темп прироста составит:
Отсюда следует, что при наличии темпа роста можно удобно и быстро определить темп прироста. Темпы прироста могут быть выражены положительными (+) и отрицательными (-) значениями. При этом положительные значения темпа указывают на рост последующего уровня по сравнению с предыдущим; отрицательное же значение указывает на его снижение. В последнем случае говорят о темпе снижения. Результаты исчисления базисных и цепных темпов прироста и снижения покажем на примере динамики реализованных фруктов специализированной сельскохозяйственной организацией (табл. 9.5).
Т а б л и ц а 9.5. Динамика реализации фруктов
Как видно, темпы роста и темпы прироста в динамике снижаются. Это свидетельствует об убывающем характере динамики реализованной продукции. Темпы прироста за весь изучаемый период в динамическом ряду могут быть охарактеризованы при помощи их среднего значения. При расчете среднего темпа прироста можно исходить из значения среднего темпа роста, т.е.
где Допустим, необходимо определить среднегодовой темп прироста валового сбора картофеля в фермерском хозяйстве за период 2008 – 2010 гг., если в 2008 г. было произведено 120 т, в 2010 – 150 т картофеля. Прежде всего рассчитаем средний темп валового сбора картофеля по формуле (9.11), т.е.,
Затем находим средний темп прироста производства картофеля:
Значит, ежегодный прирост валового сбора картофеля в фермерском хозяйстве за период 2008 – 2010 гг. составил в среднем 11, 8%.
Дата добавления: 2016-06-06 | Просмотры: 586 | Нарушение авторских прав |
 , (9.12)
, (9.12) . (9.13)
. (9.13)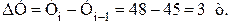 .Затем рассчитаем темп прироста:
.Затем рассчитаем темп прироста: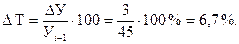
 , или
, или 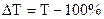 . (9.14)
. (9.14)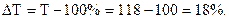
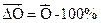 (9.15)
(9.15) –– средний темп прироста;
–– средний темп прироста; 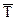 –– средний темп роста.
–– средний темп роста.