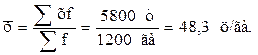АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Распределения по урожайности льносоломки

Для нахождения среднего значения признака в интервальном ряду распределения необходимые данные, приведённые в табл. 6.3, подставим в формулу (6.4), получим:

Это означает, что средняя урожайность льносоломки в сельскохозяйственных организациях района составляет 48,3 ц/га.

Если интервальный ряд, используемый для вычисления средней варианты, содержит открытые интервалы, то центры этих интервалов могут быть рассчитаны исходя из предположения, что размеры открытых интервалов совпадают с размерами последующих или предыдущих интервалов, непосредственно к ним примыкающих. При этом срединное значение первого (верхнего) открытого интервала может быть найдено путем вычитания из середины второго интервала величины этого интервала, а срединное значение последнего (нижнего) открытого интервала – прибавлением к середине предпоследнего интервала величины этого же интервала.

Необходимо иметь в виду, что исчисление средней арифметической величины по данным интервального ряда распределения не всегда является абсолютно правильным. Это объясняется неравномерным распределением вариант внутри интервала, в качестве же множителя х для каждого интервала используется его середина. Кроме того, при наличии открытых интервалов к этому добавляются неточности, связанные с установлением неизвестных границ. Поэтому рассмотренный способ расчёта средней варианты для интервального ряда целесообразно применять лишь в тех случаях, когда отсутствуют данные о значениях признака для всей совокупности в целом. При наличии же таких данных точное значение средней варианты может быть получено способом расчёта для дискретного ряда распределения.

В системе АПК средняя арифметическая величина (простая и взвешенная) широко применяется при расчёте многочисленных средних показателей, характеризующих наличие и использование производственного потенциала: средней площади землепользования, посевной площади, урожайности, поголовья, продуктивности животных, численности работников, производительности труда, себестоимости продукции, уровня рентабельности и многих других показателей.

Дата добавления: 2016-06-06 | Просмотры: 405 | Нарушение авторских прав